一些有用的文档：2020-5-12 %版

GitHub地址

公式部分请见Github

2020.5.12

2023.4.23

前言

一份可以用于 ACM 和 OI 的模版，有问题或建议请留言QAQ

不断更新（挖坑）中

感谢付老师、小黄老师、郑老师和 QDD 的大力滋兹，Orz%%%

基础

通用模版

#include<bits/stdc++.h>
#define endl "\n" //防止卡endl
#define rg register int //循环变量专用
#pragma GCC optimize("Ofast,no-stack-protector") //神仙优化，比较假
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<string>
#include<vector>
#include<stack>
#include<map>
#include<ctime>
using namespace std;

int main()
{
    freopen("input.in", "r", stdin);
    freopen("output.out", "w", stdout);
    
    ios::sync_with_stdio(false); //cin、cout不能与scanf、printf混用 
    cin.tie(0); //输入一定要在输出之前
    cout.tie(0);
    
    printf("%.5lf", (double)clock() / CLOCKS_PER_SEC);//输出时间
    return 0;
}

性能测试

//用已经AC了的题交这个代码，以测试评测机性能
int a;
for (int i = 0; i < 1000000000; i++) a ^= i;
cout << a;

玄学优化

#pragma GCC optimize ("O3") //开O3
#pragma GCC -mcmodle=large //开巨型数组不RE(编译时间变长)

// 以下慎用
#pragma GCC optimize(2)
#pragma GCC optimize(3)
#pragma GCC optimize("Ofast")
#pragma GCC optimize("inline")
#pragma GCC optimize("-fgcse")
#pragma GCC optimize("-fgcse-lm")
#pragma GCC optimize("-fipa-sra")
#pragma GCC optimize("-ftree-pre")
#pragma GCC optimize("-ftree-vrp")
#pragma GCC optimize("-fpeephole2")
#pragma GCC optimize("-ffast-math")
#pragma GCC optimize("-fsched-spec")
#pragma GCC optimize("unroll-loops")
#pragma GCC optimize("-falign-jumps")
#pragma GCC optimize("-falign-loops")
#pragma GCC optimize("-falign-labels")
#pragma GCC optimize("-fdevirtualize")
#pragma GCC optimize("-fcaller-saves")
#pragma GCC optimize("-fcrossjumping")
#pragma GCC optimize("-fthread-jumps")
#pragma GCC optimize("-funroll-loops")
#pragma GCC optimize("-freorder-blocks")
#pragma GCC optimize("-fschedule-insns")
#pragma GCC optimize("inline-functions")
#pragma GCC optimize("-ftree-tail-merge")
#pragma GCC optimize("-fschedule-insns2")
#pragma GCC optimize("-fstrict-aliasing")
#pragma GCC optimize("-falign-functions")
#pragma GCC optimize("-fcse-follow-jumps")
#pragma GCC optimize("-fsched-interblock")
#pragma GCC optimize("-fpartial-inlining")
#pragma GCC optimize("no-stack-protector")
#pragma GCC optimize("-freorder-functions")
#pragma GCC optimize("-findirect-inlining")
#pragma GCC optimize("-fhoist-adjacent-loads")
#pragma GCC optimize("-frerun-cse-after-loop")
#pragma GCC optimize("inline-small-functions")
#pragma GCC optimize("-finline-small-functions")
#pragma GCC optimize("-ftree-switch-conversion")
#pragma GCC optimize("-foptimize-sibling-calls")
#pragma GCC optimize("-fexpensive-optimizations")
#pragma GCC optimize("inline-functions-called-once")
#pragma GCC optimize("-fdelete-null-pointer-checks")

手动扩栈

//C++使用，在开头写
#pragma comment(linker, "/STACK:1024000000,1024000000")

//G++使用
#include <bits/stdc++.h>
using namespace std;

extern void MAIN(void) __asm__("MAIN");
void MAIN()
{
    //在这里写代码
    exit(0);
}

int main()
{
    long long size = 4096ll << 20; // 4096 MB
    char* p = new char[size] + size;
    __asm__ __volatile__(
        "movq %0, %%rsp\n"
        "pushq $exit\n"
        "jmp MAIN\n"
        ::"r"(p));
    MAIN();
}

输入输出

特殊格式与转换

char s[MAX];
scanf(" %[^\n]", s);    //遇到回车结束（读一整行）
scanf(" %[^#]", s);     //遇到#结束     
scanf(" %[^ ]", s);     //遇到空格结束

char str[20];
cin.getline(name); //读入一行
cin.getline(name, 20); //读入一行，指定长度

string s;
getline(cin, s); //string的读入一行

//读到文件尾
while (cin) {}
while(~scanf) {}

// 输出为二进制
cout << "x = " << bitset<32>(x) << endl;

// 十进制转换十六进制
stringstream ss;
ss << hex << stol("123");
string hex_num = ss.str();

精度控制

//设置有效数字位数。
cout << setprecision(位数) << number << endl;

//设置小数精度(小数点后的有效位数)
cout <<setiosflags(ios::fixed);    
cout << setprecision(位数) << number << endl;

//设置小数精度(小数点后的有效位数)
cout << fixed << setprecision(10) << number << endl;

挂

// 本机测试需要EOF才能看到输出结果

// 快速输入挂
// 读入1e7 大约0.4s
namespace fastinput
{
#define BUF_SIZE 1048576

    inline char nc()
    {
        static char buf[BUF_SIZE], *p1 = buf + BUF_SIZE, *pend = buf + BUF_SIZE;
        if (p1 == pend)
        {
            p1 = buf;
            pend = buf + fread(buf, 1, BUF_SIZE, stdin);
            assert(pend != p1);
        }
        return *p1++;
    }

    inline bool blank(char c) { return c == ' ' || c == '\n' || c == '\r' || c == '\t'; }

    // non-negative integer
    inline int get_unsigned_int()
    {
        int x = 0;
        char c = nc();
        while (blank(c)) c = nc();
        for (; c >= '0' && c <= '9'; c = nc()) x = x * 10 + c - '0';
        return x;
    }

    // integer
    inline int get_int()
    {
        int x = 0, sgn = 1;
        char c = nc();
        while (blank(c)) c = nc();
        if (c == '-') sgn = -1, c = nc();
        for (; c >= '0' && c <= '9'; c = nc()) x = x * 10 + c - '0';
        return sgn * x;
    }

#undef BUF_SIZE
};

//使用
using namespace fastinput;
int n = get_int();
unsigned int n = get_unsigned_int();

//输入输出挂
namespace fastIO
{
#define BUF_SIZE 100000
#define OUT_SIZE 100000
#define ll long long
    //fread->read
    bool IOerror = 0;
    inline char nc()
    {
        static char buf[BUF_SIZE], *p1 = buf + BUF_SIZE, *pend = buf + BUF_SIZE;
        if (p1 == pend)
        {
            p1 = buf; pend = buf + fread(buf, 1, BUF_SIZE, stdin);
            if (pend == p1) { IOerror = 1; return -1; }
            //{printf("IO error!\n"); system("pause"); for (;;); exit(0);}
        }
        return *p1++;
    }
    inline bool blank(char ch) { return ch == ' ' || ch == '\n' || ch == '\r' || ch == '\t'; }
    inline void read(int &x)
    {
        bool sign = 0; char ch = nc(); x = 0;
        for (; blank(ch); ch = nc());
        if (IOerror) return;
        if (ch == '-') sign = 1, ch = nc();
        for (; ch >= '0'&&ch <= '9'; ch = nc()) x = x * 10 + ch - '0';
        if (sign) x = -x;
    }
    inline void read(ll &x)
    {
        bool sign = 0; char ch = nc(); x = 0;
        for (; blank(ch); ch = nc());
        if (IOerror) return;
        if (ch == '-') sign = 1, ch = nc();
        for (; ch >= '0'&&ch <= '9'; ch = nc()) x = x * 10 + ch - '0';
        if (sign) x = -x;
    }
    inline void read(double &x)
    {
        bool sign = 0; char ch = nc(); x = 0;
        for (; blank(ch); ch = nc());
        if (IOerror) return;
        if (ch == '-') sign = 1, ch = nc();
        for (; ch >= '0'&&ch <= '9'; ch = nc()) x = x * 10 + ch - '0';
        if (ch == '.')
        {
            double tmp = 1; ch = nc();
            for (; ch >= '0'&&ch <= '9'; ch = nc())tmp /= 10.0, x += tmp * (ch - '0');
        }
        if (sign) x = -x;
    }
    inline void read(char *s)
    {
        char ch = nc();
        for (; blank(ch); ch = nc());
        if (IOerror) return;
        for (; !blank(ch) && !IOerror; ch = nc()) *s++ = ch;
        *s = 0;
    }
    inline void read(char &c)
    {
        for (c = nc(); blank(c); c = nc());
        if (IOerror) { c = -1; return; }
    }
    //fwrite->write
    struct Ostream_fwrite
    {
        char *buf, *p1, *pend;
        Ostream_fwrite() { buf = new char[BUF_SIZE]; p1 = buf; pend = buf + BUF_SIZE; }
        void out(char ch)
        {
            if (p1 == pend) { fwrite(buf, 1, BUF_SIZE, stdout); p1 = buf; }
            *p1++ = ch;
        }
        void print(int x)
        {
            static char s[15], *s1; s1 = s;
            if (!x) *s1++ = '0'; if (x < 0) out('-'), x = -x;
            while (x) *s1++ = x % 10 + '0', x /= 10;
            while (s1-- != s) out(*s1);
        }
        void println(int x)
        {
            static char s[15], *s1; s1 = s;
            if (!x) *s1++ = '0'; if (x < 0) out('-'), x = -x;
            while (x) *s1++ = x % 10 + '0', x /= 10;
            while (s1-- != s) out(*s1); out('\n');
        }
        void print(ll x)
        {
            static char s[25], *s1; s1 = s;
            if (!x) *s1++ = '0'; if (x < 0) out('-'), x = -x;
            while (x) *s1++ = x % 10 + '0', x /= 10;
            while (s1-- != s) out(*s1);
        }
        void println(ll x)
        {
            static char s[25], *s1; s1 = s;
            if (!x) *s1++ = '0'; if (x < 0) out('-'), x = -x;
            while (x) *s1++ = x % 10 + '0', x /= 10;
            while (s1-- != s) out(*s1); out('\n');
        }
        void print(double x, int y)
        {
            static ll mul[] = { 1,10,100,1000,10000,100000,1000000,10000000,100000000, 1000000000,10000000000LL,100000000000LL,1000000000000LL,10000000000000LL, 100000000000000LL,1000000000000000LL,10000000000000000LL,100000000000000000LL };
            if (x < -1e-12) out('-'), x = -x; x *= mul[y];
            ll x1 = (ll)floor(x); if (x - floor(x) >= 0.5) ++x1;
            ll x2 = x1 / mul[y], x3 = x1 - x2 * mul[y]; print(x2);
            if (y > 0) { out('.'); for (size_t i = 1; i < y&&x3*mul[i] < mul[y]; out('0'), ++i); print(x3); }
        }
        void println(double x, int y) { print(x, y); out('\n'); }
        void print(char *s) { while (*s) out(*s++); }
        void println(char *s) { while (*s) out(*s++); out('\n'); }
        void flush() { if (p1 != buf) { fwrite(buf, 1, p1 - buf, stdout); p1 = buf; } }
        ~Ostream_fwrite() { flush(); }
    } Ostream;
    inline void print(int x) { Ostream.print(x); }
    inline void println(int x) { Ostream.println(x); }
    inline void print(char x) { Ostream.out(x); }
    inline void println(char x) { Ostream.out(x); Ostream.out('\n'); }
    inline void print(ll x) { Ostream.print(x); }
    inline void println(ll x) { Ostream.println(x); }
    inline void print(double x, int y) { Ostream.print(x, y); }
    inline void println(double x, int y) { Ostream.println(x, y); }
    inline void print(char *s) { Ostream.print(s); }
    inline void println(char *s) { Ostream.println(s); }
    inline void println() { Ostream.out('\n'); }
    inline void flush() { Ostream.flush(); }
#undef ll
#undef OUT_SIZE
#undef BUF_SIZE
};

//使用
using namespace fastIO;
int n;
read(n);
print(n);
println(n);

参考

ASCII表

这里

ASCII表

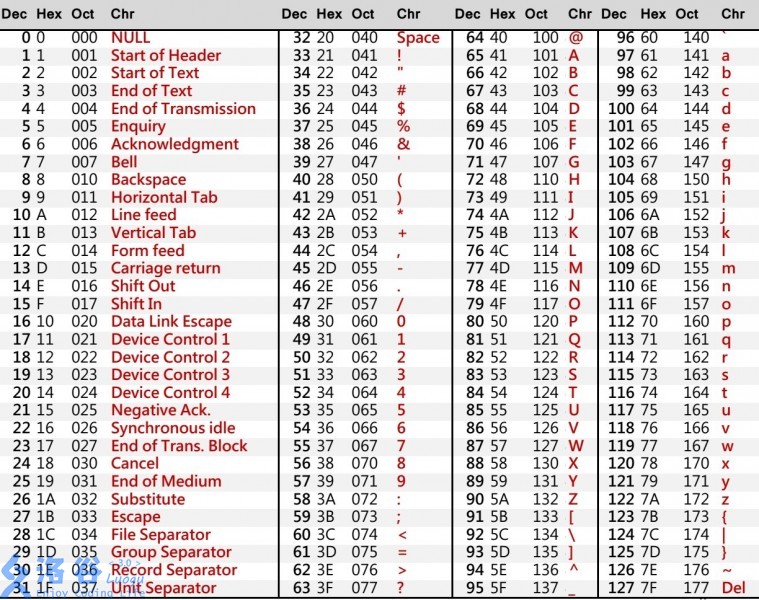
常用数表

类型	数据
char	-128 ~ 127
short	-32768 ~ 32767
int	-2147483648 ~ 2147483647(±2e9)
unsigned int	-0 ~ 4294967295(4e9)
long long	-9223372036854775808 ~ 9223372036854775807(±9e18)
unsigned long long	0 ~ 18446744073709551615(1e19)
double	± (1.7e-308 ~ 1.7e308)
long double	± (1.2e-4932 ~ 1.2e4932)
INF = 0x3f3f3f3f	1061109567
LINF = 0x3f3f3f3f3f3f3f3f	4557430888798830399

时间复杂度与数据规模

评测机每秒约 $10^8$ 至 $1.5 \times 10^9$

1MB内存约 $2.5 \times 10^5$ 也就是 25万个int（4个字节）

数学

常用网站

数学理论

负数求余

负数的求余数仍为负数，有正负时使用if (abs(x%2))或者if (x&1)判断是否为奇数

组合数

通项公式:

$$
C_{m}^{n}=\frac{m !}{n ! *(m-n) !}
$$

递推公式:

$$
C_{m}^{n}=C_{m-1}^{n}+C_{m-1}^{n-1}
$$

性质:

$$
C_{m+r+1}^{r}=\sum_{i=0}^{r} C_{m+i}^{i}
$$

$$
C_{m}^{n} * C_{n}^{r}=C_{m}^{r} * C_{m-r}^{n-r}
$$

$$
\sum_{i=0}^{m} C_{m}^{i} * x^{i}=(x+1)^{m}
$$

$$
C_{m}^{0}-C_{m}^{1}+C_{m}^{2}-\ldots \pm C_{m}^{m}=0
$$

$$
C_{m}^{0}+C_{m}^{2}+C_{m}^{4} \ldots=C_{m}^{1}+C_{m}^{3}+C_{m}^{5}+\ldots=2^{m-1}
$$

$$
C_{m+n}^{r}=C_{m}^{0} * C_{n}^{r}+C_{m}^{1} * C_{n}^{r-1}+\ldots+C_{m}^{r} * C_{n}^{0}
$$

$$
C_{m+n}^{n}=C_{m}^{0} * C_{n}^{0}+C_{m}^{1} * C_{n}^{1}+\ldots+C_{m}^{m} * C_{n}^{m}
$$

$$
n * C_{m}^{n}=m * C_{m-1}^{n-1}
$$

$$
\sum_{i=1}^{n} C_{n}^{i} * i=n * 2^{n-1}
$$

$$
\sum_{i=1}^{n} C_{n}^{i} * i^{2}=n *(n+1) * 2^{n-2}
$$

$$
\sum_{i=0}^{n}\left(C_{n}^{i}\right)^{2}=C_{2 n}^{n}
$$

奇偶性: 对于 $C_{n}^{k}$ ，若 n & k = k 则 $C_{n}^{k}$ 为奇数，否则为偶数。

错位排列数

将数字1~n排成一列，且数字i不在第i位的方案数:

$$
D_1=0\ ,\ D_2=1
$$

$$
D_n=(n-1)(D_{n-1}+D_{n-2})
$$

威尔逊定理

当且仅当p为质数时，有

$$
(p-1) ! \equiv -1 \mod{p}
$$

$$
(p-1) ! \equiv p-1 \mod{p}
$$

费马小定理

若p是质数，则对于任意整数a，有

$$
a^{p-1}\equiv 1 \mod{p}
$$

$$
a^{p}\equiv a \mod{p}
$$

费马大定理

当整数 $n>2$ 时，方程

$$
x^n+y^n=z^n
$$

无正整数解

哥德巴赫猜想

任一大于2的偶数都可写成两个素数之和

任一大于5的奇数都可写成三个素数之和

勾股数

$$
a^2+b^2=c^2
$$

当 $n>1$ 时:

$$
a=2n+1,b=2n^2+2n,c=2n^2+2n+1
$$

$$
a=2n,b=n^2-1,c=n^2+1
$$

$$
a=4n,b=4n^2-1,c=4n^2+1\ (a,b,c 互质)
$$

抽屉原理

原理一：把n+1个咕咕咕放到n个巢里，那么至少有两个咕咕咕在同一个巢里

原理二：把m*n-1个物体放入n个抽屉中，其中必定有一个抽屉中最多有m-1个物体 (例如：将3×5-1=14个物体放入5个抽屉中，则必定有一个抽屉中的物体数少于等于3-1=2)

欧拉公式

对于简单多面体（或者投射），点-边+面=2

$$
V-E+F=2
$$

欧几里德算法

最大公约数 GCD

1 2	//欧几里德算法 gcd(a,b) == gcd(b,a%b) int gcd(int x, int y) { return y ? gcd(y, x%y) : x; }

扩展欧几里德算法 EXGCD

裴蜀等式

对任意两个整数a和b，关于未知数x和y的线性丢番图方程（裴蜀等式）：

$$
ax+by=m
$$

当且仅当m是gcd(a,b)的倍数时有整数解(x,y)。裴蜀等式有解时必然有无穷多个解。

推论：a,b互质时使得 $ax+by=1$ 有解（充要条件）

扩展欧几里德算法

用于求裴蜀等式的特解 $(x_0,y_0)$ ，即 $ax+by=gcd(a,b)$ 的解(绝对值之和最小的解)。

原式 $ax+by=m$ 的通解 k∈z

$$
x=\frac{m}{gcd(a,b)}x_0+k\frac{b}{gcd(a,b)}
$$

$$
y=\frac{m}{gcd(a,b)}y_0-k\frac{a}{gcd(a,b)}
$$

//x,y为引用，返回值为gcd(a,b)
int exgcd(int a, int b, int &x, int &y)
{
    if (b == 0)
    {
        x = 1;
        y = 0;
        return a;
    }
    int r = exgcd(b, a%b, x, y);
    int t = y;
    y = x - (a / b) * y;
    x = t;
    return r;
}

欧拉

欧拉函数

定义

对于一个正整数x，小于x且和x互质的正整数（包括1）的个数，记作 $φ(x)$

$$
φ(x)=x\prod_{i=1}^{n}(1-\frac{1}{p_i})
$$

性质

对于质数p， $φ(p)=p-1$ ，且 $φ(1)=1$

对于质数p，有 $n=p^k$ ，则 $φ(n)=p^k-p^{k-1}=(p-1)p^{k-1}$

对于奇数p， $φ(2p)=φ(p)$

对于一个正整数n，与其互质的数之和为 $φ(n)*n/2$

对于一个正整数n，对于所有n的正整数因子d (即 $d|n$ )，即 $\sum_{d|n} φ(d)=n$

对于一个正整数n，且a为n的质因数，则：

若 $n|a$ 且 $(n/a)|a$ ，则 $φ(n)=φ(n/a)*a$

若 $n|a$ 且 $(n/a) \nmid a$，则 $φ(n)=φ(n/a)*(a-1)$

积性函数：若m,n互质(即 $gcd(m,n)=1$ )，则 $φ(mn)=φ(m)φ(n)=(m-1)(n-1)$

求法

直接求

//O(sqrt())
int phi(int x)
{
    int res = x, a = x;
    for (int i = 2; i*i <= a; i++)
        if (a%i == 0)
        {
            res = res / i * (i - 1);
            while (a%i == 0) a /= i;
        }
    if (a > 1) res = res / a * (a - 1);
    return res;
}

线性筛法

//较快，O(n)
//更快的请参考杜教筛
const static int MAXN = 50000 + 100;
bool check[MAXN];
int phi[MAXN] = { 0 }, prime[MAXN] = { 0 };
void get_phi()
{
    memset(check, false, sizeof(check));
    int tot = 0;
    phi[1] = 1;
    for (int i = 2; i <= MAXN - 100; ++i)
    {
        if (!check[i])
        {
            prime[tot++] = i;
            phi[i] = i - 1;
        }
        for (int j = 0; j < tot; ++j)
        {
            if (i * prime[j] > MAXN - 100) break;
            check[i * prime[j]] = true;
            if (i % prime[j] == 0)
            {
                phi[i * prime[j]] = phi[i] * prime[j];
                break;
            }
            else phi[i * prime[j]] = phi[i] * (prime[j] - 1);
        }
    }
}

递推法

//较慢
const static int MAXN = 50000 + 100;
int phi[MAXN] = { 0 };
void get_phi()
{
    phi[1] = 1;
    for (int i = 2; i <= MAXN - 100; i++)
        if (!phi[i])
            for (int j = i; j <= MAXN - 100; j += i)
            {
                if (!phi[j]) phi[j] = j;
                phi[j] = phi[j] / i * (i - 1);
            }
}

欧拉定理

若正整数a, n互质($gcd(a,p)=1$)，则

$$
a^{φ(n)}\equiv1\pmod{n}
$$

欧拉降幂

对于 $x\geqφ(p)$，有

$$
a^x \equiv a^{(x \ mod \ φ(p))+φ(p)}\pmod{p}
$$

对于 $x<φ(p)$ ，无需降幂。

欧拉路径

欧拉回路

每条边只经过一次，且回到起点

无向图：连通（不考虑度为0的点），每个顶点度数都为偶数
有向图：基图连通（把边当成无向边，同样不考虑度为0的点），每个顶点的出度等于入度
混合图：
- 既有无向边也有向边，首先是基图连通（不考虑度为0的点），然后需要借助网络流判定。
- 首先给原图中的每条无向边随便指定一个方向（称为初始定向），将原图改为有向图G’，然后的任务就是改变G’中某些条边的方向（当然是无向边转化来的，原来混合图中的有向边不能动）使其满足每个点的入度等于出度。
- 设D[i]为G’中（点i的出度-点i的入度），即可发现，在改变G’中边的方向的过程中，任何点的D值的奇偶性都不会发生改变（设将边<i, j>改为<j, i>，则i入度加1出度减1，j入度减1出度加1，两者之差加2或者减2，奇偶性不变），而最终要求的是每个点的入度等于出度，即每个点的D值都为0，是偶数，可得：若初始定向得到的G’中任⼀个点D值是奇数，那么原图中一定不存在欧拉环。
- 若初始D值都是偶数，则将G’改装成网络：设源点S和汇点T，对于每个D[i] > 0的点i，连边<S, i>，容量为D[i]/2；对于每个D[j] < 0的点j，连边<j, T>，容量为-D[j]/2；G’中的每条边在网中仍保留，容量为i（表示该边最多只能被改变一次方向）。求这个网络的最大流，若S引出的所有边均满流，则原混合图是欧拉图，将网络中所有流量为1的中间边（就是不与S或T关联的边）在G’中改变方向，形成的新图G”一定是有向欧拉图；若S引出的边中有的没有满流，则原混合图不是欧拉图。

欧拉路径

每条边只经过一次，不要求回到起点。

无向图：连通（不考虑度为0的点），每个顶点度数都为偶数或者仅有两个点的度数为奇数。
有向图：基图连通（把边当成无向边，同样不考虑度为0的点），每个顶点出度等于入度或者有且仅有一个点的出度比入度多1，有且仅有一个点的出度比入度少1，其余的出度等于入度。
混合图：如果存在欧拉回路，一定存在欧拉路径，否则如果有且仅有两个点的（出度-入度）是奇数，那么给这两个点加边，判断是否存在欧拉回路，如果存在就一定存在欧拉路径。

杜教筛

//积性函数，欧拉函数和莫比乌斯函数
//复杂度O(n^2/3)~O(n^3/4)
const int MAXN = 2000100;
long long prime[MAXN];
long long mu[MAXN];
map<int, long long> ans_mu;

void init()
{
    fill(prime, prime + MAXN, 1);
    mu[1] = 1;
    int tot = 0;
    for (int i = 2; i < MAXN; i++)
    {
        if (prime[i])
        {
            prime[++tot] = i;
            mu[i] = -1;
        }
        for (int j = 1; j <= tot && i * prime[j] < MAXN; j++)
        {
            prime[i * prime[j]] = 0;
            if (i % prime[j] == 0)
            {
                mu[i * prime[j]] = 0;
                break;
            }
            else mu[i * prime[j]] = -mu[i];
        }
    }
    for (int i = 2; i < MAXN; i++) mu[i] += mu[i - 1];
}

long long calc_mu(int x)
{
    if (x < MAXN) return mu[x];
    if (ans_mu.count(x)) return ans_mu[x];
    long long ans = 1;
    for (long long i = 2, j; i <= x; i = j + 1)
    {
        j = x / (x / i);
        ans -= (j - i + 1) * calc_mu(x / i);
    }
    return ans_mu[x] = ans;
}

long long calc_phi(int x)
{
    long long ans = 0;
    for (long long i = 1, j; i <= x; i = j + 1)
    {
        j = x / (x / i);
        ans += (x / i) * (x / i) * (calc_mu(j) - calc_mu(i - 1));
    }
    return ((ans - 1) >> 1) + 1;
}

扩展大步小步 Baby Steps Giant Steps

用于求解高次同余方程，即求解x：

$$
a^{x} \equiv b \mod{m}
$$

普通版要求m为质数（或者a与m互质），如果x有解，则 $0 \leq x \lt m$；扩展版无要求

下列代码数据范围 $0 \leq a, b \leq m \leq 10^9 $

//北上广深算法

const long long MOD = 1313131;
const long long MAXN = 500000 + 5; // sqrt(p)

long long gcd(long long x, long long y) { return y ? gcd(y, x%y) : x; }
void Exgcd(long long a, long long b, long long &d, long long &x, long long &y)
{
    if (!b)
    {
        d = a;
        x = 1;
        y = 0;
    }
    else
    {
        Exgcd(b, a % b, d, y, x);
        y -= x * (a / b);
    }
}

long long qkpow(long long a, long long b, long long m)//O(logN) a^b%m
{
    long long ans = 1;
    a %= m;
    while (b)
    {
        if (b & 1) ans = (ans*a) % m;
        a = (a*a) % m;
        b >>= 1;
    }
    return ans % m;
}

struct Hashset
{
    long long head[MOD], Next[MAXN], f[MAXN], v[MAXN], ind;
    void reset()
    {
        ind = 0;
        memset(head, -1, sizeof head);
    }
    void Insert(long long x, long long _v)
    {
        long long ins = x % MOD;
        for (long long j = head[ins]; j != -1; j = Next[j])
            if (f[j] == x)
            {
                v[j] = min(v[j], _v);
                return;
            }
        f[ind] = x, v[ind] = _v;
        Next[ind] = head[ins], head[ins] = ind++;
    }
    long long operator [] (const long long &x) const
    {
        long long ins = x % MOD;
        for (long long j = head[ins]; j != -1; j = Next[j])
            if (f[j] == x) return v[j];
        return -1;
    }
} S;


long long Solve(long long a, long long b, long long c)
{
    long long d, x, y;
    Exgcd(a, c, d, x, y);
    x = (x + c) % c;
    return x * b % c;
}

long long BSGS(long long C, long long A, long long B, long long p)  // A^x%p=B S.T.(A,p)=1
{
    if (p <= 100)
    {
        long long d = 1;
        for (int i = 0; i < p; ++i)
        {
            if (d == B) return i;
            d = d * A % p;
        }
        return -1;
    }
    else
    {
        long long m = (int)sqrt(p);
        S.reset();
        long long d = 1, Search;
        for (int i = 0; i < m; ++i)
        {
            S.Insert(d, i);
            d = d * A % p;
        }
        for (int i = 0; i * m < p; i++)
        {
            d = qkpow(A, i * m, p) * C % p;
            Search = S[Solve(d, B, p)];
            if (Search != -1) return i * m + Search;
        }
        return -1;
    }
}

int main()
{
    long long a, b, m;
    int T;
    cin >> T;
    while (T--)
    {
        cin >> a >> b >> m;
        long long d = 1;
        bool find = 0;
        for (long long i = 0; i < 100; i++)
        {
            if (d == b)
            {
                cout << i << endl;
                find = 1;
                break;
            }
            d = d * a % m;
        }
        if (find) continue;
        long long t, C = 1, num = 0;
        while ((t = gcd(a, m)) != 1)
        {
            m /= t;
            b /= t;
            C = C * a / t % m;
            num++;
        }
        long long res = BSGS(C, a, b, m);
        if (res == -1) cout << "No Solution" << endl;
        else cout << res + num << endl;
    }
    return 0;
}

二次剩余

求二次同余方程的解 $x$ ，其中 $p$ 为奇质数：

$$
x^{2} \equiv n\ (\bmod \ p)
$$

long long quick_mod(long long a, long long b, long long m)
{
    long long ans = 1;
    a %= m;
    while (b)
    {
        if (b & 1)
        {
            ans = ans * a % m;
            b--;
        }
        b >>= 1;
        a = a * a % m;
    }
    return ans;
}

struct T
{
    long long p, d;
};

long long w;

//二次域乘法
T multi_er(T a, T b, long long m)
{
    T ans;
    ans.p = (a.p * b.p % m + a.d * b.d % m * w % m) % m;
    ans.d = (a.p * b.d % m + a.d * b.p % m) % m;
    return ans;
}

//二次域上快速幂
T power(T a, long long b, long long m)
{
    T ans;
    ans.p = 1;
    ans.d = 0;
    while (b)
    {
        if (b & 1)
        {
            ans = multi_er(ans, a, m);
            b--;
        }
        b >>= 1;
        a = multi_er(a, a, m);
    }
    return ans;
}

//求勒让德符号
long long Legendre(long long a, long long p) { return quick_mod(a, (p - 1) >> 1, p); }

long long mod(long long a, long long m)
{
    a %= m;
    if (a < 0) a += m;
    return a;
}

long long Solve(long long n, long long p)
{
    if (p == 2) return 1;
    if (Legendre(n, p) + 1 == p) return -1;
    long long a = -1, t;

    srand(time(nullptr));
    while (true)
    {
        a = rand() % p;
        t = a * a - n;
        w = mod(t, p);
        if (Legendre(w, p) + 1 == p) break;
    }
    T tmp;
    tmp.p = a;
    tmp.d = 1;
    T ans = power(tmp, (p + 1) >> 1, p);
    return ans.p;
}

int main()
{
    // x*x = a (mod n)

    long long a, n;
    cin >> a >> n;
    a %= n;

    auto ans1 = Solve(a, n);
    auto ans2 = n - ans1;

    if (ans1 == -1) cout << "No root" << endl;
    else if (ans1 == ans2) cout << ans1 << endl;
    else cout << ans1 << " " << ans2 << endl;

    return 0;
}

快速傅里叶变换 FFT

多项式乘法

//计算多项式乘法F(x)*G(x)
/*
输入
第一行2个正整数n, m
第二行n + 1个数字，从低到高表示F(x)的系数
第三行m + 1个数字，从低到高表示G(x)的系数
例子：
1 2
1 2
1 2 1

输出
一行n+m+1个数字，从低到高表示F(x)∗G(x)的系数
例子：
1 4 5 2

F(x) = 1 + 2*x
G(x) = 1 + 2*x + x^2
F(x)*G(x) = 1 + 4*x + 5*x^2 + 2*x^3
*/
#define rg register int
const int MAXN = 10000001;
const double pi = acos(-1);

struct Complex
{
    double r, i;
    Complex() {}
    Complex(double a, double b) :r(a), i(b) {}
    Complex operator + (const Complex B) const { return Complex(r + B.r, i + B.i); }
    Complex operator - (const Complex B) const { return Complex(r - B.r, i - B.i); }
    Complex operator * (const Complex B) const { return Complex(r*B.r - i * B.i, r*B.i + i * B.r); }
};

Complex X, Y, a[MAXN], b[MAXN];
int r[MAXN], n, m, l;

inline void FFT(Complex *a, int x)
{
    for (rg i = 0; i < n; i++)
        if (i < r[i]) swap(a[i], a[r[i]]);
    for (rg i = 1; i < n; i <<= 1)
    {
        Complex wn(cos(pi / i), x*sin(pi / i));
        for (rg j = 0; j < n; j += (i << 1))
        {
            Complex w(1, 0);
            for (rg k = 0; k < i; ++k, w = w * wn)
            {
                X = a[j + k], Y = a[i + j + k] * w;
                a[j + k] = X + Y, a[i + j + k] = X - Y;
            }
        }
    }
    if (x == -1)
        for (rg i = 0; i < n; i++) a[i].r = a[i].r / n;
}

int main()
{
    scanf("%d%d", &n, &m);
    for (rg i = 0; i <= n; i++) scanf("%lf", &a[i].r);
    for (rg i = 0; i <= m; i++) scanf("%lf", &b[i].r);
    m += n;
    for (n = 1; n <= m; n <<= 1) l++;
    for (rg i = 0; i < n; i++)
        r[i] = (r[i >> 1] >> 1) | ((i & 1) << (l - 1));
    FFT(a, 1);
    FFT(b, 1);
    for (rg i = 0; i <= n; i++) a[i] = a[i] * b[i];
    FFT(a, -1);
    for (rg i = 0; i <= m; i++)
        printf("%d ", (int)(a[i].r + 0.5));
    return 0;
}

相同位数整数乘法

/*
输入
位数
整数1
整数2
*/

#define rg register int
const int MAXN = 1000001;
const long double pi = acos(-1);

struct Complex
{
    double r, i;
    Complex() {}
    Complex(double a, double b) :r(a), i(b) {}
    Complex operator + (const Complex B) const { return Complex(r + B.r, i + B.i); }
    Complex operator - (const Complex B) const { return Complex(r - B.r, i - B.i); }
    Complex operator * (const Complex B) const { return Complex(r*B.r - i * B.i, r*B.i + i * B.r); }
};

Complex X, Y, a[MAXN], b[MAXN];
int n, m, l, r[MAXN];

inline void FFT(Complex *a, int x)
{
    for (rg i = 0; i < n; i++)
        if (i < r[i]) swap(a[i], a[r[i]]);
    for (rg i = 1; i < n; i <<= 1)
    {
        Complex wn(cos(pi / i), x*sin(pi / i));
        for (rg j = 0; j < n; j += (i << 1))
        {
            Complex w(1, 0);
            for (rg k = 0; k < i; ++k, w = w * wn)
            {
                X = a[j + k], Y = a[i + j + k] * w;
                a[j + k] = X + Y, a[i + j + k] = X - Y;
            }
        }
    }
    if (x == -1) for (rg i = 0; i < n; i++) a[i].r = a[i].r / n;
}

char ch1[MAXN], ch2[MAXN];
int res[MAXN];
int main()
{
    scanf("%d", &n);
    cin >> ch1;
    cin >> ch2;
    for (rg i = 0; i < n; i++)
    {
        a[i].r = ch1[n - i - 1] - '0';
        b[i].r = ch2[n - i - 1] - '0';
    }
    m = n + n - 2;
    for (n = 1; n <= m; n <<= 1) l++;
    for (rg i = 0; i < n; i++)
        r[i] = (r[i >> 1] >> 1) | ((i & 1) << (l - 1));
    FFT(a, 1);
    FFT(b, 1);
    for (rg i = 0; i <= n; i++) a[i] = a[i] * b[i];
    FFT(a, -1);
    for (rg i = 0; i <= m; i++) res[i] = (int)(a[i].r + 0.5);
    for (rg i = 0; i <= m; i++) res[i + 1] += res[i] / 10, res[i] %= 10;
    rg top = m + 1;
    while (res[top] > 9)
    {
        res[top + 1] = res[top] / 10;
        res[top] %= 10;
        top++;
    }
    while (!res[top]) top--;
    for (rg i = top; i >= 0; i--)
        printf("%d", res[i]);
    return 0;
}

任意整数乘法

//较复杂
//时间较慢
const int maxn = 500100; //至少是数据长度的4倍
const double PI = acos(-1.0);

struct Complex
{
    double r, i;
    Complex(double _r = 0.0, double _i = 0.0) { r = _r; i = _i; }
    Complex operator + (const Complex &b) { return Complex(r + b.r, i + b.i); }
    Complex operator - (const Complex &b) { return Complex(r - b.r, i - b.i); }
    Complex operator * (const Complex &b) { return Complex(r*b.r - i * b.i, r*b.i + i * b.r); }
};

void change(Complex y[], int len)
{
    int k;
    for (int i = 1, j = len / 2; i < len - 1; i++)
    {
        if (i < j) swap(y[i], y[j]);
        k = len / 2;
        while (j >= k)
        {
            j -= k;
            k /= 2;
        }
        if (j < k) j += k;
    }
}

//做FFT，len必须为2^k形式，on==1时是DFT，on==-1时是IDFT
void fft(Complex y[], int len, int on)
{
    change(y, len);
    for (int h = 2; h <= len; h <<= 1)
    {
        Complex wn(cos(-on * 2 * PI / h), sin(-on * 2 * PI / h));
        for (int j = 0; j < len; j += h)
        {
            Complex w(1, 0);
            for (int k = j; k < j + h / 2; k++)
            {
                Complex u = y[k];
                Complex t = w * y[k + h / 2];
                y[k] = u + t;
                y[k + h / 2] = u - t;
                w = w * wn;
            }
        }
    }
    if (on == -1)
        for (int i = 0; i < len; i++) y[i].r /= len;
}

char num1[maxn], num2[maxn];
Complex x1[maxn], x2[maxn];
int ans[maxn];

int main()
{
    while (cin >> num1 >> num2)
    {
        memset(ans, 0, sizeof(ans));
        int len = 1, len1 = strlen(num1), len2 = strlen(num2);
        while (len < len1 + len2 + 1) len <<= 1;
        for (int i = 0; i < len1; i++) x1[len1 - 1 - i] = Complex((double)(num1[i] - '0'), 0);
        for (int i = len1; i < len; i++) x1[i] = Complex(0, 0);
        fft(x1, len, 1);
        for (int i = 0; i < len2; i++) x2[len2 - 1 - i] = Complex((double)(num2[i] - '0'), 0);
        for (int i = len2; i < len; i++) x2[i] = Complex(0, 0);
        fft(x2, len, 1);
        for (int i = 0; i < len; i++) x1[i] = x1[i] * x2[i];
        fft(x1, len, -1);
        for (int i = 0; i < len; i++) ans[i] = (int)(x1[i].r + 0.5);
        
        // 进位
        for (int i = 1; i < len; i++)
        {
            ans[i] += ans[i - 1] / 10;
            ans[i - 1] %= 10;
        }
        while (len > 0 && !ans[len]) len--;
        for (int i = len; i >= 0; i--) printf("%c", ans[i] + '0');
        printf("\n");
    }
    return 0;
}

快速幂

//O(logN) x^n
double qkpow(double x, int n)
{
    const auto flag = n >= 0;
    auto pow = abs(static_cast<long long>(n));
    double ans = 1;

    while (pow)
    {
        if (pow & 1) ans *= x;
        x *= x;
        pow >>= 1;
    }

    return flag ? ans : 1 / ans;
}

long long qkpow(long long x, long long n, const long long mod)
{
    long long ans = 1;
    x %= mod;

    while (n)
    {
        if (n & 1) ans = (ans * x) % mod;
        x = (x * x) % mod;
        n >>= 1;
    }

    return ans % mod;
}

斐波那契数列

通项：

$$
a_{1}=1, a_{2}=1, a_{n}=a_{n-1}+a_{n-2}\left(n \geq 3, n \in N^{*}\right)
$$

$$
a_{n}=1 / \sqrt{5}\left[\left(\frac{1+\sqrt{5}}{2}\right)^{n}-\left(\frac{1-\sqrt{5}}{2}\right)^{n}\right]
$$

// 求第n项，模mod
#define mod(a, m) ((a) % (m) + (m)) % (m)
const int MOD = 1e9 + 9;

struct MATRIX
{
    long long a[2][2];
};

MATRIX a;
long long f[2];

void ANS_Cf(MATRIX a)
{
    f[0] = mod(a.a[0][0] + a.a[1][0], MOD);
    f[1] = mod(a.a[0][1] + a.a[1][1], MOD);
}

MATRIX MATRIX_Cf(MATRIX a, MATRIX b)
{
    MATRIX ans;
    int k;
    for (int i = 0; i < 2; i++)
    {
        for (int j = 0; j < 2; j++)
        {
            ans.a[i][j] = 0;
            k = 0;
            while (k < 2)
            {
                ans.a[i][j] += a.a[k][i] * b.a[j][k];
                ans.a[i][j] = mod(ans.a[i][j], MOD);
                ++k;
            }
        }
    }
    return ans;
}

MATRIX MATRIX_Pow(MATRIX a, long long n)
{
    MATRIX ans;
    ans.a[0][0] = 1;
    ans.a[1][1] = 1;
    ans.a[0][1] = 0;
    ans.a[1][0] = 0;
    while (n)
    {
        if (n & 1) ans = MATRIX_Cf(ans, a);
        n = n >> 1;
        a = MATRIX_Cf(a, a);
    }
    return ans;
}

int fib(long long n)
{
    if (n == 1) return 1;
    a.a[0][0] = a.a[0][1] = a.a[1][0] = 1;
    a.a[1][1] = 0;
    a = MATRIX_Pow(a, n - 2);
    ANS_Cf(a);
    return f[0];
}

素数

试商法

//试商法
bool isPrime(const int x)
{
    if (x < 2) return false;
    for (auto i = 2; i * i <= x; i++)
        if (x % i == 0) return false;
    return true;
}

打表法

//O(n*loglogn)
const auto n = 1000;
int a[n + 5] = {1, 1};
vector<int> v;
for (auto i = 2; i <= n; i++)
    for (auto j = i * 2; j <= n; j += i) a[j] = 1;
for (auto i = 1; i <= n; i++)
    if (a[i] == 0) v.emplace_back(i); // 素数 a[i]==0

素因子

直接求

// 查询数的所有不重复素因子
// 暴力 O(sqrt(n))
void getf(vector<int> &v, int x)
{
    for (int i = 2; i * i <= x; i++)
    {
        if (x % i == 0)
        {
            v.push_back(i);
            while (x % i == 0) x /= i;
        }
        if (x == 1) break;
    }
    if (x != 1) v.push_back(x);
}

// 对数进行分解质因数
void getf(vector<int> &v, int x)
{
    for (int i = 2; i * i <= x; i++)
    {
        while (x % i == 0)
        {
            v.push_back(i);
            x /= i;
        }
        if (x == 1) break;
    }
    if (x != 1) v.push_back(x);
}

打表法

// 筛每个数的最小素因子
// 预处理 O(nloglogn)
const int MAXN = 100000 + 50;
int spf[MAXN];

void init_spf()
{
    for (int i = 2; i < MAXN - 5; i++)
    {
        if (!spf[i])
        {
            for (int j = i; j < MAXN - 5; j += i)
            {
                if (!spf[j]) spf[j] = i;
            }
        }
    }
}

// O(logn)
// 查询数的所有不重复素因子
void getf(vector<int> &v, int x)
{
    while (x > 1)
    {
        int p = spf[x];
        v.push_back(p);
        while (x % p == 0) x /= p;
    }
}

// 对数进行分解质因数
void getf(vector<int> &v, int x)
{
    while (x > 1)
    {
        int p = spf[x];
        while (x % p == 0)
        {
            v.push_back(p);
            x /= p;
        }
    }
}

逆元

定义

如果有 $a*b\equiv 1 \pmod{p}$ 且 $gcd(a,p)=1$ （a与p互质），则称b是模p意义下a的乘法逆元，记 $b=inv(a)$ 或 $b=a^{−1}$

(定义了模意义下的除法运算：除以一个数取模等于乘以这个数的逆元取模)

求法

费马小定理

由费马小定理得 $a^p-a \equiv 0 \pmod{p}$

即 $a^p \equiv a \pmod{p}$

即 $a^{p-1} \equiv 1 \pmod{p}$

即 $a*a^{p-2} \equiv 1 \pmod{p}$

当模数p为质数时， $a^{p-2}$ 即为a在模p意义下的逆元，快速幂求解即可，时间复杂度O(logn)

//模数MOD为质数
const long long MOD = 1e9 + 7;

long long powMod(long long a, long long b)
{
    long long ans = 1;
    for (a %= MOD; b; b >>= 1)
    {
        if (b & 1) ans = ans * a % MOD;
        a = a * a % MOD;
    }
    return ans;
}

long long inv(long long x) { return powMod(x, MOD - 2); }

扩展欧几里得法

//扩展欧几里得法，gcd(a, MOD) = 1时有逆元
//O(logn)
const long long MOD = 1e9 + 7;
long long exgcd(long long a, long long b, long long &x, long long &y)
{
    if (b == 0)
    {
        x = 1;
        y = 0;
        return a;
    }
    long long d = exgcd(b, a % b, y, x);
    y -= a / b * x;
    return d;
}

long long inv(long long a)
{
    long long x, y;
    long long d = exgcd(a, MOD, x, y);
    if (d == 1) return (x % MOD + MOD) % MOD;
    else return -1;
}

打表法

const long long MOD = 1e9 + 7;
long long inv[10000];
void initInv()
{
    inv[1] = 1;
    for (int i = 2; i < 10000; i++)
    {
        inv[i] = 1LL * (MOD - MOD / i) * inv[MOD % i] % MOD;
    }
}

中国剩余定理

孙子定理：有物不知其数，三三数之剩二，五五数之剩三，七七数之剩二。问物几何？

求解同余方程组

$$
\left{\begin{array}{l}{x \equiv a_{1}\left(\bmod m_{1}\right)} \ {x \equiv a_{2}\left(\bmod m_{2}\right)} \ {x \equiv a_{3}\left(\bmod m_{3}\right)} \ {\ldots} \ {x \equiv a_{k}\left(\bmod m_{k}\right)}\end{array}\right.
$$

其中 $m_{1}, m_{2}, m_{3} \dots m_{k}$ 为两两互质的整数

求 $x$ 的最小非负整数解

解：

令 $M=\prod_{i=1}^{k} m_{i}$ ，即 $M$ 是所有 $m_i$ 的最小公倍数

$t_i$ 为 $\frac{M}{m_{i}}$ 模 $m_i$ 的逆元，即 $\frac{M}{m_{i}} t_{i} \equiv 1\left(\bmod m_{i}\right)$ 的最小非负整数解

则有一个解为 $x=\sum_{i=1}^{k} a_{i} \frac{M}{m_{i}} t_{i}$

通解为 $x+i * M(i \in Z)$

特别的，最小非负整数解为 (x%M+M)%M

int china()
{
    int k; // 方程组数
    vector<int> m; //方程中的m
    vector<int> a; //方程中的a

    int ans = 0, lcm = 1, x, y;
    for (int i = 1; i <= k; ++i) lcm *= m[i];
    for (int i = 1; i <= k; ++i)
    {
        int tp = lcm / m[i];
        exgcd(tp, m[i], x, y);
        x = (x % m[i] + m[i]) % m[i]; //x要为最小非负整数解
        ans = (ans + tp * x * a[i]) % lcm;
    }
    return (ans + lcm) % lcm;
}

整数运算

大整数

//2的n次方可以用pow直接算
//UTF-8 使用限定
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <algorithm>
#include <vector>
#include <list>
#include <map>
#include <cstring>
#include <string>
#include <iostream>
#include <fstream>
#include <cmath>
using namespace std;

#define BIGNUM_DEBUG 2333

class Bignum
{
    void mknum(const char *s, int len = -1)
    {
        sign = 0;
        if (*s == '-')
        {
            mknum(s + 1);
            sign = 1;
            return;
        }
        int l;
        if (len == -1) l = strlen(s);
        else l = len;
        l = strlen(s);
        bits.clear();
        bits.resize(l);
        for (int i = l - 1; i >= 0; i--) bits[l - i - 1] = s[i] - '0';
        maintain();
    }
    void mknum(string &s) { mknum(s.c_str(), s.length()); }
    ///////////////////////////////////////////////////////////////////
    void us_addto(Bignum &b)  // unsigned add to
    {
        int mlen = max(b.bits.size(), bits.size());
        int slen = bits.size();
        int olen = b.bits.size();
        bits.resize(mlen);
        for (int i = 0; i < mlen; i++)
        {
            int s = 0;
            if (i < slen)s += bits[i];
            if (i < olen)s += b.bits[i];
            bits[i] = s;
        }
        maintain();
    }
    class FFTer
    {
        class Complex
        {
        public:
            double real, image;
            Complex(double a = 0, double b = 0)
            {
                real = a;
                image = b;
            }
            Complex operator + (const Complex &o) { return Complex(real + o.real, image + o.image); }
            Complex operator - (const Complex &o) { return Complex(real - o.real, image - o.image); }
            Complex operator * (const Complex &o) { return Complex(real*o.real - image * o.image, real*o.image + o.real*image); }
            Complex operator * (double k) { return Complex(real*k, image*k); }
            Complex operator / (double k) { return Complex(real / k, image / k); }
        };
    public:
        vector<Complex> a;  //系数向量
        int n;              //多项式次数上界
        FFTer(vector<int> &vec)
        {
            a.resize(vec.size());
            for (int i = 0; i < vec.size(); i++) a[i].real = vec[i];
            n = vec.size();
        }
        void transform()
        {
            int j = 0;
            int k;
            for (int i = 0; i < n; i++)
            {
                if (j > i) swap(a[i], a[j]);
                k = n;
                while (j & (k >>= 1)) j &= ~k;
                j |= k;
            }
        }
        void FFT(bool IDFT = false)
        {
            const double Pi = IDFT ? -acos(-1.0) : acos(-1.0);
            //IDFT与DFT选择方向相反（符号相反）
            transform();//交换元素（翻转二进制位，具体看下面注释，再具体看算导
            for (int s = 1; s < n; s <<= 1)
                //算法导论上是fot s = 1 to lgn,考虑到精度问题改为上面那个...
                for (int t = 0; t < n; t += s << 1)
                {
                    //合并[t, t+s-1]与 [t+s, t+2*s-1] (算导上以指数形式给出，注意到他的s....)
                    //合并为[t, t+2*s-1] (看起来像是废话) (有示例图在算导上，画得很形象的)
                    double x = Pi / s;
                    Complex omgn(cos(x), sin(x));
                    Complex omg(1.0, 0.0);    //单位向量
                    for (int m = 0; m < s; m++)
                    {            //旋转
                        int a1 = m + t;
                        int a2 = m + t + s;   //取两边系数向量的系数
                        //算导上管这个叫公共子表达式消除
                        //其实就是一个变量计算一次然后保存下来用多次
                        Complex comm = omg * a[a2];
                        a[a2] = a[a1] - comm;
                        a[a1] = a[a1] + comm;  //这两个顺序不要反了
                        omg = omg * omgn;
                    }
                }
            if (IDFT)
                for (int i = 0; i < n; i++) a[i] = a[i] / n;
        }
        void mul(FFTer &o)
        {
            int s = 1;
            while (s < n + o.n)s <<= 1;
            n = o.n = s;
            a.resize(s);
            o.a.resize(s);
            FFT(false);
            o.FFT(false);
            for (int i = 0; i < n; i++) a[i] = a[i] * o.a[i];
            FFT(true);
        }
    };
    void us_multo(Bignum &b)
    {
        FFTer x(bits);
        FFTer y(b.bits);
        x.mul(y);
        bits.clear();
        bits.resize(x.a.size());
        for (int i = 0; i < x.n; i++) bits[i] = (int)(x.a[i].real + 0.5);
        maintain();
    }
    void us_multo_simu(Bignum &b)
    {
        vector<int> r;
        r.resize(max(length(), b.length()) << 1);
        for (int i = 0; i < length(); i++)
            for (int j = 0; j < b.length(); j++) r[i + j] += bits[i] * b.bits[j];
        *(&(this->bits)) = r;
        maintain();
    }
    void us_subto(Bignum &b) // abs(self) >= abs(other)
    {
        int mlen = length();
        int olen = b.length();
        for (int i = 0; i < mlen; i++)
        {
            int s = bits[i];
            if (i < olen) s -= b.bits[i];
            bits[i] = s;
            if (bits[i] < 0)
            {
                bits[i] += 10;
                bits[i + 1] -= 1;
            }
        }
        for (int i = bits.size() - 1; !bits[i] && i >= 1; i--) bits.pop_back();
        if (bits.size() == 1 && bits[0] == 0) sign = 0;
    }
    void us_divto(Bignum &b)
    {
        if (length() == 1 && bits[0] == 0) return;
        Bignum L("0");
        L.sign = 0;
        Bignum R(*this);
        R.sign = 0;
        Bignum two("2");
        R *= two;
        Bignum one("1");
        one.sign = 0;
        while (L + one != R)
        {
            Bignum M = L + R;
            M.divto2();
            Bignum t = M * b;
            if (t > *this) R = M;
            else if (t < *this) L = M;
            else
            {
                *this = M;
                L = M;
                break;
            }
        }
        *this = L;
    }
public:
    int sign;
    vector<int> bits;
    int length() { return bits.size(); }
    void maintain()
    {
        for (int i = 0; i < bits.size(); i++)
        {
            if (i + 1 < bits.size()) bits[i + 1] += bits[i] / 10;
            else if (bits[i] > 9) bits.push_back(bits[i] / 10);
            bits[i] %= 10;
        }
        if (bits.size() == 0)
        {
            bits.push_back(0);
            sign = 0;
        }
        for (int i = bits.size() - 1; !bits[i] && i >= 1; i--) bits.pop_back();
    }

    Bignum(string &s)
    {
        Bignum();
        mknum(s);
    }
    Bignum(const char *s)
    {
        Bignum();
        mknum(s);
    }
    Bignum(int n)
    {
        Bignum();
        char buf[15];
        sprintf(buf, "%d", n);
        mknum(buf);
    }
    Bignum()
    {
        sign = 0;
        bits.push_back(0);
    }
    Bignum(const Bignum& b)
    {
        copy(b);
    }
    void copy(const Bignum& b)
    {
        sign = b.sign;
        bits = b.bits;
    }
    ///////////////////////////////////////////////////
    bool us_cmp(Bignum &b)   //无符号的比较
    {
        if (length() != b.length()) return false;
        int l = length();
        for (int i = 0; i < l; i++)
            if (bits[i] != b.bits[i]) return false;
        return true;
    }
    bool us_larger(Bignum &b)
    {
        if (length() > b.length()) return true;
        else if (length() < b.length()) return false;
        int l = length();
        for (int i = l - 1; i >= 0; i--)
            if (bits[i] > b.bits[i]) return true;
            else if (bits[i] < b.bits[i]) return false;
        return false;
    }
    bool operator == (Bignum &o)
    {
        if (sign != o.sign) return false;
        return us_cmp(o);
    }
    bool operator != (Bignum &o) { return !(*this == o); }
    bool operator > (Bignum &o)
    {
        if (sign == 0 && o.sign == 1) return true;
        if (sign == 1 && o.sign == 0) return false;
        if (sign == o.sign && sign) return !us_larger(o);
        return us_larger(o);
    }
    bool operator < (Bignum &o)
    {
        return !(*this == o || *this > o);   //小于就是不等于也不大于
    }
    bool operator <= (Bignum &o)
    {
        return *this < o || *this == o;
    }
    bool operator >= (Bignum &o)
    {
        return *this > o || *this == o;
    }
    ////////////////////////////////////////////////////
    Bignum& operator += (Bignum &o)
    {
        if (!sign && !o.sign)
        {
            us_addto(o);
            sign = 0;
        }
        else if (sign && o.sign)
        {
            us_addto(o);
            sign = 1;
        }
        else if (sign && !o.sign)
        {
            if (o.us_larger(*this))
            {
                Bignum t(o);
                t.us_subto(*this);
                *this = t;
                sign = 0;
            }
            else
            {
                us_subto(o);
                sign = 1;
                if (bits.size() == 1 && bits[0] == 0) sign = 0;
            }
        }
        else if (!sign && o.sign)
        {
            if (us_larger(o))
            {
                us_subto(o);
                sign = 0;
            }
            else
            {
                Bignum t(o);
                t.us_subto(*this);
                *this = t;
                sign = 1;
                if (bits.size() == 1 && bits[0] == 0) sign = 0;
            }
        }
        return *this;
    }
    Bignum operator + (Bignum &o)
    {
        Bignum t(*this);
        t += o;
        return t;
    }
    /////////////////////////////////////////////////
    Bignum& operator*= (Bignum &o)
    {
        if (length() + o.length() > 800) us_multo(o); //FFT
        else us_multo_simu(o);                          //simulate
        if (sign == o.sign) sign = 0;
        else sign = 1;
        return *this;
    }
    Bignum operator* (Bignum &o)
    {
        Bignum t(*this);
        t *= o;
        return t;
    }
    ////////////////////////////////////////////////
    Bignum& operator-= (Bignum &o)
    {
        if (!sign && !o.sign)
        {
            if (us_larger(o))
            {
                us_subto(o);
                sign = 0;
            }
            else
            {
                Bignum t(o);
                t.us_subto(*this);
                *this = t;
                sign = 1;
                if (bits.size() == 1 && bits[0] == 0) sign = 0;
            }
        }
        else if (sign && o.sign)
        {
            if (us_larger(o))
            {
                us_subto(o);
                sign = 1;
                if (bits.size() == 1 && bits[0] == 0) sign = 0;
            }
            else
            {
                Bignum t(o);
                t.us_subto(*this);
                *this = t;
                sign = 0;
            }
        }
        else if (!sign && o.sign)
        {
            us_addto(o);
            sign = 0;
        }
        else if (sign && !o.sign)
        {
            us_addto(o);
            sign = 1;
        }
        return *this;
    }
    Bignum operator - (Bignum &o)
    {
        Bignum t(*this);
        t -= o;
        return t;
    }
    ///////////////////////////////////////////////
    Bignum& divto2()
    {
        if (!bits.size()) return *this;
        bits[0] >>= 1;
        int i;
        for (i = 1; i < bits.size(); i++)
        {
            if (bits[i] & 1) bits[i - 1] += 5;
            bits[i] >>= 1;
        }
        if (bits[i - 1] == 0) bits.pop_back();
        return *this;
    }
    Bignum& operator /= (Bignum &o)
    {
        us_divto(o);
        if (sign == o.sign) sign = 0;
        else sign = 1;
        return *this;
    }
    Bignum operator / (Bignum &o)
    {
        Bignum t(*this);
        t /= o;
        return t;
    }
    //////////////////////////////////////////
    Bignum abs()
    {
        Bignum t(*this);
        t.sign = 0;
        return t;
    }

    Bignum sqrt()
    {
        Bignum L("0"), R(*this);
        Bignum one("1");
        Bignum m, t;
        while (L + one != R)
        {
            m = L + R;
            m.divto2();
            Bignum t = m * m;
            if (t == *this) return m;
            else if (t > *this) R = m;
            else L = m;
        }
        return L;
    }

    //若e <= 0则会返回1
    //底数（也就是this）是负数的话会根据次数决定符号
    Bignum pow(Bignum &e) //a^b == a.pow(b)
    {
        if (e.sign)return 1;
        Bignum ans("1");
        Bignum base(*this);
        Bignum zero("0");
        Bignum exp(e);
        while (exp > zero)
        {
            if (exp.bits[0] & 1) ans *= base;
            base *= base;
            exp.divto2();
        }
        if (sign && e.bits[0] & 1) ans.sign = 1;
        return ans;
    }

    //注意，如果本数小于底数返回1...
    Bignum log(Bignum &base)
    {
        if (sign) return 0;
        if (length() == 1 && bits[0] == 1) return 0;
        if (*this <= base) return 1;
        Bignum one("1");
        Bignum r("1");
        Bignum c("0");
        while (r < *this)
        {
            r *= base;
            c += one;
        }
        if (r != *this) c -= one;
        return c;
    }
    Bignum lg()
    {
        Bignum ten("10");
        return log(ten);
    }

    Bignum factorial()
    {
        Bignum r("1");
        Bignum zero("0");
        Bignum one("1");
        Bignum t(*this);
        while (t > zero)
        {
            r *= t;
            t -= one;
        }
        return r;
    }

    /////////////////////////////////////////////////////////
    friend istream& operator >> (istream &is, Bignum &b)
    {
        string s;
        is >> s;
        b.mknum(s);
        return is;
    }
    friend ostream& operator << (ostream &os, Bignum b)
    {
        if (b.sign)os << '-';
        for (int i = b.bits.size() - 1; i >= 0; i--) os << b.bits[i];
        return os;
    }

    string to_string()
    {
        int sz = length();
        string s;
        if (sign) s.resize(sz + 1);
        else s.resize(sz);
        int i = 0;
        if (sign) s[i++] = '-';
        for (int j = sz - 1; i < sz + sign; i++, j--) s[i] = bits[j] + '0';
        return s;
    }

};
////////////////////////////
#ifdef BIGNUM_DEBUG
#ifdef __GNUC__
__attribute__((noinline))     //禁止内联
#endif
#ifdef __MINGW32__
__attribute__((noinline))
#endif
char* printB(Bignum &b)
{
    //仅仅是用于能在gdb中使用它来输出自己
    string s = b.to_string();
    char *buf = (char *)malloc(sizeof(char) * s.length());
    //这个函数仅用于调试，这里申请的内存不会释放
    //因此非调试时不要使用这个函数
    strcpy(buf, s.c_str());
    return buf;  //然后gdb中就可以 print printB(一个Bignum )
}
#endif

int main()
{
    Bignum a;
    cin >> a;
    a = a * a;
    cout << a;
    return 0;
}

自动取模

template<long long MOD>
class mod_number
{
public:
    mod_number() : x(0) {}

    mod_number(long long _) { x = (_ % MOD + MOD) % MOD; }

private:
    long long x;

    mod_number pow(long long n)
    {
        mod_number a = *this, ans = 1;
        while (n)
        {
            if (n & 1) ans *= a;
            n >>= 1;
            a *= a;
        }
        return ans;
    }

    mod_number inv() { return pow(MOD - 2); }

public:
    mod_number operator+(const mod_number &y) { return mod_number(x + y.x); }

    mod_number operator-(const mod_number &y) { return mod_number(x - y.x); }

    mod_number operator*(const mod_number &y) { return mod_number(x * y.x); }

    mod_number operator/(mod_number y) { return mod_number(mod_number(x) * y.inv()); }

    mod_number &operator+=(const mod_number &y) { return *this = *this + y; }

    mod_number &operator-=(const mod_number &y) { return *this = *this - y; }

    mod_number &operator*=(const mod_number &y) { return *this = *this * y; }

    mod_number &operator/=(mod_number y) { return *this = *this / y; }

    const mod_number operator++(int)
    {
        mod_number temp(x);
        *this += 1;
        return temp;
    }

    const mod_number operator--(int)
    {
        mod_number temp(x);
        *this -= 1;
        return temp;
    }

    mod_number operator++() { return *this += 1; }

    mod_number operator--() { return *this -= 1; }

    bool operator<(const mod_number &y) { return x < y.x; }

    bool operator>(const mod_number &y) { return x > y.x; }

    bool operator<=(const mod_number &y) { return x <= y.x; }

    bool operator>=(const mod_number &y) { return x >= y.x; }

    bool operator==(const mod_number &y) { return x == y.x; }

    bool operator!=(const mod_number &y) { return x != y.x; }

    mod_number operator[](int) { return inv(); }

    friend std::ostream &operator<<(std::ostream &os, const mod_number &y) { return os << y.x; }

    friend std::istream &operator>>(std::istream &is, mod_number &y)
    {
        is >> y.x;
        if (!is) y = mod_number();
        else y = mod_number(y.x);
        return is;
    }
};

//声明
const long long IntMaxn = 19260817; //此处为质数
using Int = ModInt<IntMaxn>;

//使用
//for循环请不要用Int做循环变量
Int a, b[10];       //声明数与数组
cin>>a;             //输入
cout<<a;            //输出
Int x=Int(1);       //类型转换
Int(a).pow(b.x);    //快速幂，a的b次方
q.inv();            //q的乘法逆元

求N!的最后一位的非0数

const int ff[] = {1, 1, 2, 6, 4, 4, 4, 8, 4, 6};

int fact(int n)
{
    int i, x;
    if (n < 5) return ff[n];
    x = (ff[n % 10] * 6) % 10;
    for (i = 1; i <= (n / 5) % 4; i++)
        if (x == 6 || x == 2) x = (x + 10) / 2;
        else x /= 2;
    return (fact(n / 5) * x) % 10;
}

星期问题

基姆拉尔森公式

$$
W = (D + 2M + 3(M + 1) / 5 + Y + Y / 4 - Y / 100 + Y / 400) \mod 7
$$

// 已知1752年9月3日是Sunday，并且日期控制在1700年2月28日后
char name[][15] = {
    "monday", "tuesday", "wednesday", "thursday", "friday", "saturday",
    "sunday"
};

int main()
{
    int d, m, y, a;
    printf("Day: ");
    scanf("%d", &d);
    printf("Month: ");
    scanf("%d", &m);
    printf("Year: ");
    scanf("%d", &y);
    // 一二月当做前一年的十三十四月
    if (m == 1 || m == 2)
    {
        m += 12;
        y--;
    }
    // 判断是否在1752年9月3日之前
    if ((y < 1752) || (y == 1752 && m < 9) || (y == 1752 && m == 9 && d < 3))
    {
        // 因为日期控制在1700年2月28日后，所以不用考虑整百年是否是闰年
        a = (d + 2 * m + 3 * (m + 1) / 5 + y + y / 4 + 5) % 7;
    }
    else
    {
        // 这里需要考虑整百年是否是闰年
        a = (d + 2 * m + 3 * (m + 1) / 5 + y + y / 4 - y / 100 + y / 400) % 7;
    }
    printf("it's a %s\n", name[a]);
    return 0;
}

计算几何

Pick 公式

顶点坐标均是整点的简单多边形:

面积 = 内部格点数 + 边上格点数 / 2 - 1

S = n + s / 2 - 1

(其中n表示多边形内部的点数,s表示多边形边界上的点数,S表示多边形的面积)

已知圆锥表面积S求最大体积V

$$
V = S \times \sqrt{\frac{S}{72\pi}}
$$

常用

struct Point
{
    double x, y;
    Point(double x = 0, double y = 0) : x(x), y(y) {}
    Point operator + (Point p) { return Point(x + p.x, y + p.y); }
    Point operator - (Point p) { return Point(x - p.x, y - p.y); }
};
typedef Point Vector;
double getDot(Vector a, Vector b) { return a.x * b.x + a.y * b.y; }    // 点积
double getCross(Vector a, Vector b) { return a.x * b.y - a.y * b.x; }  // 叉积
double getLength(Vector a) { return sqrt(getDot(a, a)); }              // 模

// 绕原点逆时针旋转角度B（弧度值）
void transXY(Point &p, double B)
{
    double x = p.x, y = p.y;
    p.x = x * cos(B) - y * sin(B);
    p.y = x * sin(B) + y * cos(B);
}

// 判断三点共线（整数值）
bool isCollinear(const Point &d1, const Point &d2, const Point &d)
{
    long long f = 1LL * (d.x - d2.x) * (d1.y - d2.y);
    long long g = 1LL * (d.y - d2.y) * (d1.x - d2.x);
    return f == g;
}

凸多边形宽度

//平行切线间的最小距离
//多边形的最小的长度
const int MAXN = 115; //点的数量

struct P
{
    int x, y;
    P() {}
    P (int _x, int _y) { x = _x, y = _y; }
    P operator - (P b) { return P(x - b.x, y - b.y); }
    double len() { return hypot(x, y); }
} a[MAXN];

double cross(P a, P b) { return a.x*b.y - a.y*b.x; }
double dist(P p, P a, P b) { return cross(p - a, b - a) / (b - a).len(); }

double min_len(int n)
{
    double ans = 1e100;
    for (int i = 1; i <= n; i++)
        for (int j = 1; j < i; j++)
        {
            double l = 1e100, r = -1e100;
            for (int k = 1; k <= n; k++)
            {
                l = min(l, dist(a[k], a[i], a[j]));
                r = max(r, dist(a[k], a[i], a[j]));
            }
            r -= l;
            ans = min(ans, r);
        }
    return ans;
}

int main()
{
    int n;
    cin >> n;
    for (int i = 1; i <= n; i++) cin>>a[i].x>>a[i].y;
    printf("%.10f\n", min_len(n));

    return 0;
}

凸包,图形,交点,交线,数学,半平面交

#include <cstdio>
#include <cstring>
#include <cmath>
#include <vector>
#include <complex>
#include <algorithm>

using namespace std;
typedef pair<int,int> pii;
const double pi = 4 * atan(1);
const double eps = 1e-10;

inline int dcmp (double x) { if (fabs(x) < eps) return 0; else return x < 0 ? -1 : 1; }
inline double getDistance (double x, double y) { return sqrt(x * x + y * y); }
inline double torad(double deg) { return deg / 180 * pi; }

struct Point {
    double x, y;
    Point (double x = 0, double y = 0): x(x), y(y) {}
    void read () { scanf("%lf%lf", &x, &y); }
    void write () { printf("%f %f", x, y); }

    bool operator == (const Point& u) const { return dcmp(x - u.x) == 0 && dcmp(y - u.y) == 0; }
    bool operator != (const Point& u) const { return !(*this == u); }
    bool operator < (const Point& u) const { return dcmp(x - u.x) < 0 || (dcmp(x-u.x)==0 && dcmp(y-u.y) < 0); }
    bool operator > (const Point& u) const { return u < *this; }
    bool operator <= (const Point& u) const { return *this < u || *this == u; }
    bool operator >= (const Point& u) const { return *this > u || *this == u; }
    Point operator + (const Point& u) { return Point(x + u.x, y + u.y); }
    Point operator - (const Point& u) { return Point(x - u.x, y - u.y); }
    Point operator * (const double u) { return Point(x * u, y * u); }
    Point operator / (const double u) { return Point(x / u, y / u); }
    double operator ^ (const Point& u) { return x*u.y - y*u.x; }
};
typedef Point Vector;
typedef vector<Point> Polygon;

struct Line {
    double a, b, c;
    Line (double a = 0, double b = 0, double c = 0): a(a), b(b), c(c) {}
};

struct DirLine {
    Point p;
    Vector v;
    double ang;
    DirLine () {}
    DirLine (Point p, Vector v): p(p), v(v) { ang = atan2(v.y, v.x); }
    bool operator < (const DirLine& u) const { return ang < u.ang; }
};

struct Circle {
    Point o;
    double r;
    Circle () {}
    Circle (Point o, double r = 0): o(o), r(r) {}
    void read () { o.read(), scanf("%lf", &r); }
    Point point(double rad) { return Point(o.x + cos(rad)*r, o.y + sin(rad)*r); }
    double getArea (double rad) { return rad * r * r / 2; }
};


namespace Punctual {
    double getDistance (Point a, Point b) { double x=a.x-b.x, y=a.y-b.y; return sqrt(x*x + y*y); }
};


namespace Vectorial {
    /* 点积: 两向量长度的乘积再乘上它们夹角的余弦, 夹角大于90度时点积为负 */
    double getDot (Vector a, Vector b) { return a.x * b.x + a.y * b.y; }

    /* 叉积: 叉积等于两向量组成的三角形有向面积的两倍, cross(v, w) = -cross(w, v) */
    double getCross (Vector a, Vector b) { return a.x * b.y - a.y * b.x; }

    double getLength (Vector a) { return sqrt(getDot(a, a)); }
    double getPLength (Vector a) { return getDot(a, a); }
    double getAngle (Vector u) { return atan2(u.y, u.x); }
    double getAngle (Vector a, Vector b) { return acos(getDot(a, b) / getLength(a) / getLength(b)); }
    Vector rotate (Vector a, double rad) { return Vector(a.x*cos(rad)-a.y*sin(rad), a.x*sin(rad)+a.y*cos(rad)); }
    /* 单位法线 */
    Vector getNormal (Vector a) { double l = getLength(a); return Vector(-a.y/l, a.x/l); }
};

namespace ComplexVector {
    typedef complex<double> Point;
    typedef Point Vector;

    double getDot(Vector a, Vector b) { return real(conj(a)*b); }
    double getCross(Vector a, Vector b) { return imag(conj(a)*b); }
    Vector rotate(Vector a, double rad) { return a*exp(Point(0, rad)); }
};

namespace Linear {
    using namespace Vectorial;

    Line getLine (double x1, double y1, double x2, double y2) { return Line(y2-y1, x1-x2, y1*x2-x1*y2); }
    Line getLine (double a, double b, Point u) { return Line(a, -b, u.y * b - u.x * a); }

    bool getIntersection (Line p, Line q, Point& o) {
        if (fabs(p.a * q.b - q.a * p.b) < eps)
            return false;
        o.x = (q.c * p.b - p.c * q.b) / (p.a * q.b - q.a * p.b);
        o.y = (q.c * p.a - p.c * q.a) / (p.b * q.a - q.b * p.a);
        return true;
    }

    /* 直线pv和直线qw的交点 */
    bool getIntersection (Point p, Vector v, Point q, Vector w, Point& o) {
        if (dcmp(getCross(v, w)) == 0) return false;
        Vector u = p - q;
        double k = getCross(w, u) / getCross(v, w);
        o = p + v * k;
        return true;
    }

    /* 点p到直线ab的距离 */
    double getDistanceToLine (Point p, Point a, Point b) { return fabs(getCross(b-a, p-a) / getLength(b-a)); }
    double getDistanceToSegment (Point p, Point a, Point b) {
        if (a == b) return getLength(p-a);
        Vector v1 = b - a, v2 = p - a, v3 = p - b;
        if (dcmp(getDot(v1, v2)) < 0) return getLength(v2);
        else if (dcmp(getDot(v1, v3)) > 0) return getLength(v3);
        else return fabs(getCross(v1, v2) / getLength(v1));
    }

    /* 点p在直线ab上的投影 */
    Point getPointToLine (Point p, Point a, Point b) { Vector v = b-a; return a+v*(getDot(v, p-a) / getDot(v,v)); }

    /* 判断线段是否存在交点 */
    bool haveIntersection (Point a1, Point a2, Point b1, Point b2) {
        double c1=getCross(a2-a1, b1-a1), c2=getCross(a2-a1, b2-a1), c3=getCross(b2-b1, a1-b1), c4=getCross(b2-b1,a2-b1);
        return dcmp(c1)*dcmp(c2) < 0 && dcmp(c3)*dcmp(c4) < 0;
    }

    /* 判断点是否在线段上 */
    bool onSegment (Point p, Point a, Point b) { return dcmp(getCross(a-p, b-p)) == 0 && dcmp(getDot(a-p, b-p)) < 0; }
    bool onLine (Point p, Point a, Point b) { return dcmp(getCross(a-p, b-p)) == 0}
    bool onLeft(DirLine l, Point p) { return dcmp(l.v ^ (p-l.p)) >= 0; }
}

namespace Triangular {
    using namespace Vectorial;

    double getAngle (double a, double b, double c) { return acos((a*a+b*b-c*c) / (2*a*b)); }
    double getArea (double a, double b, double c) { double s =(a+b+c)/2; return sqrt(s*(s-a)*(s-b)*(s-c)); }
    double getArea (double a, double h) { return a * h / 2; }
    double getArea (Point a, Point b, Point c) { return fabs(getCross(b - a, c - a)) / 2; }
    double getDirArea (Point a, Point b, Point c) { return getCross(b - a, c - a) / 2; }
};

namespace Polygonal {
    using namespace Vectorial;
    using namespace Linear;

    double getArea (Point* p, int n) {
        double ret = 0;
        for (int i = 0; i < n-1; i++)
            ret += (p[i]-p[0]) ^ (p[i+1]-p[0]);
        return ret/2;
    }

    /* 凸包 */
    int getConvexHull (Point* p, int n, Point* ch) {
        sort(p, p + n);
        int m = 0;
        for (int i = 0; i < n; i++) {
            /* 可共线 */
            //while (m > 1 && dcmp(getCross(ch[m-1]-ch[m-2], p[i]-ch[m-1])) < 0) m--;
            while (m > 1 && dcmp(getCross(ch[m-1]-ch[m-2], p[i]-ch[m-1])) <= 0) m--;
            ch[m++] = p[i];
        }
        int k = m;
        for (int i = n-2; i >= 0; i--) {
            /* 可共线 */
            //while (m > k && dcmp(getCross(ch[m-1]-ch[m-2], p[i]-ch[m-2])) < 0) m--;
            while (m > k && dcmp(getCross(ch[m-1]-ch[m-2], p[i]-ch[m-2])) <= 0) m--;
            ch[m++] = p[i];
        }
        if (n > 1) m--;
        return m;
    }

    int isPointInPolygon (Point o, Point* p, int n) {
        int wn = 0;
        for (int i = 0; i < n; i++) {
            int j = (i + 1) % n;
            if (onSegment(o, p[i], p[j]) || o == p[i]) return 0; // 边界上
            int k = dcmp(getCross(p[j] - p[i], o-p[i]));
            int d1 = dcmp(p[i].y - o.y);
            int d2 = dcmp(p[j].y - o.y);
            if (k > 0 && d1 <= 0 && d2 > 0) wn++;
            if (k < 0 && d2 <= 0 && d1 > 0) wn--;
        }
        return wn ? -1 : 1;
    }

    /* 旋转卡壳 */
    void rotatingCalipers(Point *p, int n, vector<pii>& sol) {
        sol.clear();
        int j = 1; p[n] = p[0];
        for (int i = 0; i < n; i++) {
            while (getCross(p[j+1]-p[i+1], p[i]-p[i+1]) > getCross(p[j]-p[i+1], p[i]-p[i+1]))
                j = (j+1) % n;
            sol.push_back(make_pair(i, j));
            sol.push_back(make_pair(i + 1, j + 1));
        }
    }

    void rotatingCalipersGetRectangle (Point *p, int n, double& area, double& perimeter) {
        p[n] = p[0];
        int l = 1, r = 1, j = 1;
        area = perimeter = 1e20;

        for (int i = 0; i < n; i++) {
            Vector v = (p[i+1]-p[i]) / getLength(p[i+1]-p[i]);
            while (dcmp(getDot(v, p[r%n]-p[i]) - getDot(v, p[(r+1)%n]-p[i])) < 0) r++;
            while (j < r || dcmp(getCross(v, p[j%n]-p[i]) - getCross(v,p[(j+1)%n]-p[i])) < 0) j++;
            while (l < j || dcmp(getDot(v, p[l%n]-p[i]) - getDot(v, p[(l+1)%n]-p[i])) > 0) l++;
            double w = getDot(v, p[r%n]-p[i])-getDot(v, p[l%n]-p[i]);
            double h = getDistanceToLine (p[j%n], p[i], p[i+1]);
            area = min(area, w * h);
            perimeter = min(perimeter, 2 * w + 2 * h);
        }
    }

    /* 计算半平面相交可以用增量法，o(n^2)，初始设置4条无穷大的半平面 */
    /* 用有向直线A->B切割多边形u，返回左侧。可能退化成单点或线段 */
    Polygon cutPolygon (Polygon u, Point a, Point b) {
        Polygon ret;
        int n = u.size();
        for (int i = 0; i < n; i++) {
            Point c = u[i], d = u[(i+1)%n];
            if (dcmp((b-a)^(c-a)) >= 0) ret.push_back(c);
            if (dcmp((b-a)^(c-d)) != 0) {
                Point t;
                getIntersection(a, b-a, c, d-c, t);
                if (onSegment(t, c, d))
                    ret.push_back(t);
            }
        }
        return ret;
    }

    /* 半平面相交 */
    int halfPlaneIntersection(DirLine* li, int n, Point* poly) {
        sort(li, li + n);

        int first, last;
        Point* p = new Point[n];
        DirLine* q = new DirLine[n];
        q[first=last=0] = li[0];

        for (int i = 1; i < n; i++) {
            while (first < last && !onLeft(li[i], p[last-1])) last--;
            while (first < last && !onLeft(li[i], p[first])) first++;
            q[++last] = li[i];

            if (dcmp(q[last].v ^ q[last-1].v) == 0) {
                last--;
                if (onLeft(q[last], li[i].p)) q[last] = li[i];
            }

            if (first < last)
                getIntersection(q[last-1].p, q[last-1].v, q[last].p, q[last].v, p[last-1]);
        }

        while (first < last && !onLeft(q[first], p[last-1])) last--;
        if (last - first <= 1) { delete [] p; delete [] q; return 0; }
        getIntersection(q[last].p, q[last].v, q[first].p, q[first].v, p[last]);

        int m = 0;
        for (int i = first; i <= last; i++) poly[m++] = p[i];
        delete [] p; delete [] q;
        return m;
    }

    /* 去除多边形共线点 */
    Polygon simplify (const Polygon& poly) {
        Polygon ret;
        int n = poly.size();
        for (int i = 0; i < n; i++) {
            Point a = poly[i];
            Point b = poly[(i+1)%n];
            Point c = poly[(i+2)%n];
            if (dcmp((b-a)^(c-b)) != 0 && (ret.size() == 0 || b != ret[ret.size()-1]))
                ret.push_back(b);
        }
        return ret;
    }
};

namespace Circular {
    using namespace Linear;
    using namespace Vectorial;
    using namespace Triangular;

    /* 直线和圆的交点 */
    int getLineCircleIntersection (Point p, Point q, Circle O, double& t1, double& t2, vector<Point>& sol) {
        Vector v = q - p;
        /* 使用前需清空sol */
        //sol.clear();
        double a = v.x, b = p.x - O.o.x, c = v.y, d = p.y - O.o.y;
        double e = a*a+c*c, f = 2*(a*b+c*d), g = b*b+d*d-O.r*O.r;
        double delta = f*f - 4*e*g;
        if (dcmp(delta) < 0) return 0;
        if (dcmp(delta) == 0) {
            t1 = t2 = -f / (2 * e);
            sol.push_back(p + v * t1);
            return 1;
        }

        t1 = (-f - sqrt(delta)) / (2 * e); sol.push_back(p + v * t1);
        t2 = (-f + sqrt(delta)) / (2 * e); sol.push_back(p + v * t2);
        return 2;
    }

    /* 圆和圆的交点 */
    int getCircleCircleIntersection (Circle o1, Circle o2, vector<Point>& sol) {
        double d = getLength(o1.o - o2.o);

        if (dcmp(d) == 0) {
            if (dcmp(o1.r - o2.r) == 0) return -1;
            return 0;
        }

        if (dcmp(o1.r + o2.r - d) < 0) return 0;
        if (dcmp(fabs(o1.r-o2.r) - d) > 0) return 0;

        double a = getAngle(o2.o - o1.o);
        double da = acos((o1.r*o1.r + d*d - o2.r*o2.r) / (2*o1.r*d));

        Point p1 = o1.point(a-da), p2 = o1.point(a+da);

        sol.push_back(p1);
        if (p1 == p2) return 1;
        sol.push_back(p2);
        return 2;
    }

    /* 过定点作圆的切线 */
    int getTangents (Point p, Circle o, Vector* v) {
        Vector u = o.o - p;
        double d = getLength(u);
        if (d < o.r) return 0;
        else if (dcmp(d - o.r) == 0) {
            v[0] = rotate(u, pi / 2);
            return 1;
        } else {
            double ang = asin(o.r / d);
            v[0] = rotate(u, -ang);
            v[1] = rotate(u, ang);
            return 2;
        }
    }

    /* a[i] 和 b[i] 分别是第i条切线在O1和O2上的切点 */
    /* have some problems */
    int getTangents (Circle o1, Circle o2, Point* a, Point* b) {
        int cnt = 0;
        if (o1.r < o2.r) { swap(o1, o2); swap(a, b); }
        double d2 = getLength(o1.o - o2.o); d2 = d2 * d2;
        double rdif = o1.r - o2.r, rsum = o1.r + o2.r;
        if (d2 < rdif * rdif) return 0;
        if (dcmp(d2) == 0 && dcmp(o1.r - o2.r) == 0) return -1;

        double base = getAngle(o2.o - o1.o);
        if (dcmp(d2 - rdif * rdif) == 0) {
            a[cnt] = o1.point(base); b[cnt] = o2.point(base); cnt++;
            return cnt;
        }

        double ang = acos( rdif / sqrt(d2) );
        a[cnt] = o1.point(base+ang); b[cnt] = o2.point(base+ang); cnt++;
        a[cnt] = o1.point(base-ang); b[cnt] = o2.point(base-ang); cnt++;

        if (dcmp(d2 - rsum * rsum) == 0) {
            a[cnt] = o1.point(base); b[cnt] = o2.point(base); cnt++;
        } else if (d2 > rsum * rsum) {
            double ang = acos( rsum / sqrt(d2) );
            a[cnt] = o1.point(base+ang); b[cnt] = o2.point(pi+base+ang); cnt++;
            a[cnt] = o1.point(base-ang); b[cnt] = o2.point(pi+base-ang); cnt++;
        }
        return cnt;
    }

    /* 三点确定外切圆 */
    Circle CircumscribedCircle(Point p1, Point p2, Point p3) {
        double Bx = p2.x - p1.x, By = p2.y - p1.y;
        double Cx = p3.x - p1.x, Cy = p3.y - p1.y;
        double D = 2 * (Bx * Cy - By * Cx);
        double cx = (Cy * (Bx * Bx + By * By) - By * (Cx * Cx + Cy * Cy)) / D + p1.x;
        double cy = (Bx * (Cx * Cx + Cy * Cy) - Cx * (Bx * Bx + By * By)) / D + p1.y;
        Point p = Point(cx, cy);
        return Circle(p, getLength(p1 - p));
    }

    /* 三点确定内切圆 */
    Circle InscribedCircle(Point p1, Point p2, Point p3) {
        double a = getLength(p2 - p3);
        double b = getLength(p3 - p1);
        double c = getLength(p1 - p2);
        Point p = (p1 * a + p2 * b + p3 * c) / (a + b + c);
        return Circle(p, getDistanceToLine(p, p1, p2));
    }

    /* 三角形一顶点为圆心 */
    double getPublicAreaToTriangle (Circle O, Point a, Point b) {
        if (dcmp((a-O.o)^(b-O.o)) == 0) return 0;
        int sig = 1;
        double da = getPLength(O.o-a), db = getPLength(O.o-b);
        if (dcmp(da-db) > 0) {
            swap(da, db);
            swap(a, b);
            sig = -1;
        }

        double t1, t2;
        vector<Point> sol;
        int n = getLineCircleIntersection(a, b, O, t1, t2, sol);

        if (dcmp(da-O.r*O.r) <= 0) {
            if (dcmp(db-O.r*O.r) <= 0)  return getDirArea(O.o, a, b) * sig;

            int k = 0;
            if (getPLength(sol[0]-b) > getPLength(sol[1]-b)) k = 1;

            double ret = getArea(O.o, a, sol[k]) + O.getArea(getAngle(sol[k]-O.o, b-O.o));
            double tmp = (a-O.o)^(b-O.o);
            return ret * sig * dcmp(tmp);
        }

        double d = getDistanceToSegment(O.o, a, b);
        if (dcmp(d-O.r) >= 0) {
            double ret = O.getArea(getAngle(a-O.o, b-O.o));
            double tmp = (a-O.o)^(b-O.o);
            return ret * sig * dcmp(tmp);
        }


        double k1 = O.r / getLength(a - O.o), k2 = O.r / getLength(b - O.o);
        Point p = O.o + (a - O.o) * k1, q = O.o + (b - O.o) * k2;
        double ret1 = O.getArea(getAngle(p-O.o, q-O.o));
        double ret2 = O.getArea(getAngle(sol[0]-O.o, sol[1]-O.o)) - getArea(O.o, sol[0], sol[1]);
        double ret = (ret1 - ret2), tmp = (a-O.o)^(b-O.o);
        return ret * sig * dcmp(tmp);
    }

    double getPublicAreaToPolygon (Circle O, Point* p, int n) {
        if (dcmp(O.r) == 0) return 0;
        double area = 0;
        for (int i = 0; i < n; i++) {
            int u = (i + 1) % n;
            area += getPublicAreaToTriangle(O, p[i], p[u]);
        }
        return fabs(area);
    }
};

using namespace Polygonal;
const int maxn = 105;

int N, M;
double X[maxn], Y[maxn], PX[maxn], PY[maxn];

void init () {
    double x, y;
    scanf("%d%d", &N, &M);
    for (int i = 1; i <= N; i++) {
        X[i] = Y[i] = PX[i] = PY[i] = 0;
        for (int j = 1; j <= M; j++) {
            scanf("%lf%lf", &x, &y);
            X[i] += x, Y[i] += y;
            PX[i] += x*x, PY[i] += y*y;
        }
    }
}

二进制

状态压缩

最低位是第0位	操作
取第k位（非0则为1）	(n >> k) & 1
取后k位（同上，0~k-1位）	n & ((1 << k) – 1)
第k位取反	n ^= (1 << k)
第k位变为1	n \|= (1 << k)
第k位变为0	n &= (~(1 << k))

lowbit函数

//lowbit(x)是x的二进制表达式中最低位的1所对应的值
//6的二进制是110，所以lowbit(6)的二进制为10，即lowbit(6)=2

int lowbit(int x) { return x & (-x); }
int lowbit(int x) { return x & (x ^ (x - 1)); }

动态规划 DP

01背包

$$
F[i,v]=max{F[i−1,v],\ F[i−1,v−C_i]+W_i}
$$

从二维降到一维时应逆序进行

//二维
for i= 1 to N
    for v=Ci to V 
        F[i,v]=max{F[i−1,v],F[i−1,v−Ci]+Wi}
//一维
for i=1 to N
    for j= V to Ci
        F[j]=max{F[j],F[j−Ci]+Wi}

完全背包

01背包的一维顺序版本

多重背包

二进制优化：按照2的幂进行拆分转化为01背包

二维背包

限制条件加一维

for k=1 to K
    for v = V to 0 
        for item i in group k
            f[v]=max{F[v],F[v−Ci]+Wi}

依赖背包

选主件，对附件跑01背包，最后对主件跑01背包

区间dp

石子归并

F[i][j]=min{F[i][k]+F[k+1][j]}+Sum[i][j]
for(int i=1;i<n;i++)//枚举区间长度
        for(int j=1;j+i<=n;j++)//枚举区间左端点
                for(int k=j;k<j+i;k++)//枚举中间值k
                    DP[j][j+i]=max(DP[j][k]+DP[k+1][j+i]+Sum[i][j])

四边形优化

枚举中间值时枚举一个新数组，更新时更新该数组为新的中间值

for (long long i=1; i<n; i++)
    for (long long j=2*n-i; j>0; j--)
        for (long long k=s[j][j+i-1]; k<=s[j+1][j+i]; k++)
            if (dp[j][k]+dp[k+1][j+i]+sum[j+i]-sum[j-1] <= dp[j][j+i])
            {
                dp[j][j+i]=dp[j][k]+dp[k+1][j+i]+sum[j+i]-sum[j-1];
                s[j][j+i]=k;
            }

状压dp

把储存原始状态时应该用逆状态存放，判断时可以直接用&

二分

//求在满足条件下最大或最小的值的题目，满足单调性和有序性
//整数while(l<r)，小数一般for500次,具体次数具体分析
//时间复杂度 O(logn)，最后得到的是可行域的闭区间[l,r]

while (r>l)
{
    mid=(l+r+1)/2;                       //注意是l+r+1
    if(check(mid)==true) l=mid;
    else r=mid-1;
}

三分

// 用于单峰函数求极值
// 整数用while(l<=r)，浮点数用for
// 每次选择区间内的两个点，算完一次后去掉距离标准答案的值更远的那个点到原区间的端点的区间

int f(int x)
{
    // 求值
    int ans;

    // 适用于上凸型函数
    return ans;
    // 下凸型函数可以用INF减去f(x)
    // return INF - ans;
}

int threeDivideInt(int L, int R)
{
    while (L < R - 1)
    {
        auto mid = (L + R) / 2;
        auto mmid = (mid + R) / 2;
        if (f(mid) > f(mmid)) R = mmid;
        else L = mid;
    }

    // 返回x
    return f(L) > f(R) ? L : R;
    // 上凸型返回f(x)
    // return f(f(L) > f(R) ? L : R);
    // 下凸型返回f(x)
    // return INF - f(f(L) > f(R) ? L : R);
}

double threeDivideDouble(double low, double up)
{
    double m1, m2;
    while (up - low >= eps)
    {
        m1 = low + (up - low) / 3;
        m2 = up - (up - low) / 3;
        if (f(m1) <= f(m2)) low = m1;
        else up = m2;
    }
    return (m1 + m2) / 2;
}

数据结构

并查集

// 均摊O(1)的查找、合并
const int MAXN = 100000 + 50;

// 1下标
class union_set
{
    int par[MAXN];

    //递归查询，可能会爆栈
    int find_res(int x) { return x == par[x] ? x : par[x] = find_res(par[x]); }

    //非递归查询
    int find(int x)
    {
        auto root = x;
        while (root != par[root]) root = par[root];
        while (x != root)
        {
            const auto temp = par[x];
            par[x] = root;
            x = temp;
        }
        return root;
    }

public:
    union_set() { for (auto i = 1; i < MAXN; i++) par[i] = i; }

    //连接，par[a]=b，a的祖先指向b的祖先，b的祖先为共同的root
    void link(int x, int y) { par[find(x)] = find(y); }

    bool connected(int x, int y) { return find(x) == find(y); }
};

// 0下标
class union_set
{
    vector<int> par;

    int find_res(int x) { return x == par[x] ? x : par[x] = find_res(par[x]); }

    int find(int x)
    {
        auto root = x;
        while (root != par[root]) root = par[root];
        while (x != root)
        {
            const auto temp = par[x];
            par[x] = root;
            x = temp;
        }
        return root;
    }

public:
    union_set(const int size) : par(size)
    {
        for (auto i = 0; i < size; i++) par[i] = i;
    }

    void link(int x, int y) { par[find(x)] = find(y); }

    bool connected(int x, int y) { return find(x) == find(y); }
};

单调栈

//用途：O(n)，找到从左/右遍历第一个比它小/大的元素的位置
//一个元素向左遍历的第一个比它小的数的位置就是将它插入单调栈时栈顶元素的值，若栈为空，则说明不存在这么一个数。然后将此元素的下标存入栈，就能类似迭代般地求解后面的元素

//对于a[i],l[i]表示 第i个数向左遍历的第一个比它小的元素的位置，0表示无
int a[10], l[10], n;
stack <int> S;
for (int i = 1; i <= n; i++)
{
    while (S.size() && a[S.top()] >= a[i]) S.pop();
    if (S.empty()) l[i] = 0;
    else l[i] = S.top();
    S.push(i);
}

区间最值查询 RMQ

//用于离线区间查询最大值和最小值
//ST表实现
const static int MAXN = 50000 + 100;
const static int LOGMAXN = (int)(log2(MAXN)) + 5;

int n;
int d[MAXN] = { 0 };
int dlog[MAXN] = { 0 }; //log表
int dmax[MAXN][LOGMAXN] = { 0 };
int dmin[MAXN][LOGMAXN] = { 0 };

//预处理，O(nlogn)
void init()
{
    for (int i = 1; i <= n; i++)
    {
        dmin[i][0] = d[i];
        dmax[i][0] = d[i];
    }
    for (int j = 1; (1 << j) <= n; j++)
        for (int i = 1; i + (1 << j) - 1 <= n; i++)
        {
            dmin[i][j] = min(dmin[i][j - 1], dmin[i + (1 << (j - 1))][j - 1]);
            dmax[i][j] = max(dmax[i][j - 1], dmax[i + (1 << (j - 1))][j - 1]);
        }
    for (int i = 2; i <= MAXN - 100; i++) dlog[i] = dlog[i >> 1] + 1;
}

// 数组0下标！！！
// 注意题目是否是0下标，否则查询的时候应减一后传入函数

const static int MAXN = 50000 + 100;
int nums[MAXN] = { 0 };

struct TStTable
{

    const static int LOGMAXN = (int)(log2(MAXN)) + 5;

    int stmin[MAXN][LOGMAXN] = { 0 };
    int stmax[MAXN][LOGMAXN] = { 0 };
    int XLog[LOGMAXN] = { 0 }; //log表

    TStTable()
    {
        XLog[1] = 0;
        for (int i = 2; i < LOGMAXN; i++) XLog[i] = XLog[i >> 1] + 1;
    }

    //预处理，O(nlogn)，传入数组和数字数量
    void InitSt(int *nums, int n)
    {
        for (int i = 0; i < n; i++)
        {
            stmin[i][0] = nums[i];
            stmax[i][0] = nums[i];
        }
        for (int j = 1; (1 << j) <= n; j++)
        {
            for (int i = 0; i + (1 << j) - 1 < n; i++)
            {
                stmin[i][j] = min(stmin[i][j - 1], stmin[i + (1 << (j - 1))][j - 1]);
                stmax[i][j] = max(stmax[i][j - 1], stmax[i + (1 << (j - 1))][j - 1]);
            }
        }
    }

    //查询最大值，O(1)，常数较小
    int getmax(int L, int R)
    {
        int x = XLog[R - L + 1];
        return max(stmax[L][x], stmax[R - (1 << x) + 1][x]);
    }

    //查询最小值，O(1)，常数较小
    int getmin(int L, int R)
    {
        int x = XLog[R - L + 1];
        return min(stmin[L][x], stmin[R - (1 << x) + 1][x]);
    }

    //查询最大最小值之差，O(1)，常数较小
    int getdelta(int L, int R)
    {
        int x = XLog[R - L + 1];
        return max(stmax[L][x], stmax[R - (1 << x) + 1][x]) - min(stmin[L][x], stmin[R - (1 << x) + 1][x]);
    }
} stTable;

字符串

最长回文串

//Manacher算法
//可进行回文串及信息输出
//返回值为长度
int Manacher(string &s)
{
    string s1 = "$#";
    int len0 = s.size();
    for (int i = 0; i < len0; i++)
    {
        s1 += s[i];
        s1 += "#";
    }

    int mx = 0;                //最大右边界
    int pos;                //最大回文串的对称轴
    int len = s1.size();
    vector<int> p(len);        //回文最长半径数组 p[i]=k 代表在位置i的回文串的最长半径为k
    int res = -1;            //最大长度
    for (int i = 1; i < len; i++)
    {
        if (mx > i) p[i] = min(p[2 * pos - i], mx - i); //i在mx左边
        else p[i] = 1;                                    //i在mx右边，必须一个个匹配
        while (s1[i - p[i]] == s1[i + p[i]]) p[i]++;
        if (i + p[i] > mx)                                //更新maxright 最大回文串对称轴位置
        {
            pos = i;
            mx = pos + p[i];
        }
        if (p[i] - 1 > res) res = p[i] - 1;
    }

    //字符串输出
    vector<int> ans;
    cout << "len = " << res << endl;
    for (int i = 1; i < len; i++)
        if (p[i] - 1 == res) ans.push_back((i / 2) - ((res + 1) / 2));
    cout << "num = " << ans.size() << endl;
    for (auto it : ans)
    {
        cout << "first char on: " << it << " string->";
        for (int j = it; j < it + res; j++) cout << s[j];
        cout << endl;
    }

    return res;
}

Hash处理

全字符集

//ASCII全字符集，通用版，不一定完全适用
//BASE1和BASE2应当设置为出现的字符种类数加1及以上
const long long MAXN = 100010; //字符串长度

const long long BASE1 = 257; //进制
const long long MOD1 = 32031528556843483;
//MOD数，用这个数的话单hash能过，双hash可以考虑改小这个数
//MOD数要么小于MAX_INT,要么在计算过程用快速乘

long long p1[MAXN] = { 0 };
long long Hash_1[MAXN] = { 0 };

void Hash_1_cal(string s) //求s的整个字符串的hash
{
    p1[0] = 1;
    for (int i = 1; i <= MAXN - 10; i++) p1[i] = (p1[i - 1] * BASE1) % MOD1;
    Hash_1[0] = (long long)s[0] % MOD1;
    for (int i = 1; i < s.length(); i++)
        Hash_1[i] = (Hash_1[i - 1] * BASE1 + (long long)s[i]) % MOD1;
}

long long get_H1(int l, int r) //求从子串[l,r]的哈希值
{
    return (Hash_1[r] - (l == 0 ? 0 : Hash_1[l - 1]) * p1[r - l + 1] % MOD1 + MOD1) % MOD1;
}

//双hash
const long long BASE2 = 233;
const long long MOD2 = 19260817;
//MOD数要么小于MAX_INT,要么在计算过程用快速乘

long long p2[MAXN] = { 0 };
long long Hash_2[MAXN] = { 0 };

void Hash_2_cal(string s)
{
    p2[0] = 1;
    for (int i = 1; i <= MAXN - 10; i++) p2[i] = (p2[i - 1] * BASE2) % MOD2;
    Hash_2[0] = (long long)s[0] % MOD2;
    for (int i = 1; i < s.length(); i++)
        Hash_2[i] = (Hash_2[i - 1] * BASE2 + (long long)s[i]) % MOD2;
}

long long get_H2(int l, int r)
{
    return (Hash_2[r] - (l == 0 ? 0 : Hash_2[l - 1]) * p2[r - l + 1] % MOD2 + MOD2) % MOD2;
}

小写字母集

const long long MAXN = 1700; //字符串长度
const long long BASE1 = 29; //进制
const long long MOD1 = 1e9 + 9; //MOD数
long long p1[MAXN] = { 0 };
long long Hash_1[MAXN] = { 0 };

void Hash_1_cal(string s) //求s的整个字符串的hash
{
    p1[0] = 1;
    for (int i = 1; i <= MAXN - 10; i++) p1[i] = (p1[i - 1] * BASE1) % MOD1;
    Hash_1[0] = (long long)(s[0] - 'a' + 1) % MOD1;
    for (int i = 1; i < s.length(); i++)
        Hash_1[i] = (Hash_1[i - 1] * BASE1 + (long long)(s[i] - 'a' + 1)) % MOD1;
}

long long get_H1(int l, int r) //求从子串[l,r]的哈希值
{
    return (Hash_1[r] - (l == 0 ? 0 : Hash_1[l - 1]) * p1[r - l + 1] % MOD1 + MOD1) % MOD1;
}

//双hash
const long long BASE2 = 31;
const long long MOD2 = 1e9 + 7;
long long p2[MAXN] = { 0 };
long long Hash_2[MAXN] = { 0 };

void Hash_2_cal(string s)
{
    p2[0] = 1;
    for (int i = 1; i <= MAXN - 10; i++) p2[i] = (p2[i - 1] * BASE2) % MOD2;
    Hash_2[0] = (long long)(s[0] - 'a' + 1) % MOD2;
    for (int i = 1; i < s.length(); i++)
        Hash_2[i] = (Hash_2[i - 1] * BASE2 + (long long)(s[i] - 'a' + 1)) % MOD2;
}

long long get_H2(int l, int r)
{
    return (Hash_2[r] - (l == 0 ? 0 : Hash_2[l - 1]) * p2[r - l + 1] % MOD2 + MOD2) % MOD2;
}

字符串匹配

KMP

const int MAXN = 1000;
string s, a; //在s中找a
int ans[MAXN] = {0};
int f[MAXN], slen, alen;

void getFail()
{
    int i = 0, j = -1;
    f[0] = -1;
    while (i < alen)
    {
        if (j == -1 || a[i] == a[j])
        {
            i++;
            j++;
            f[i] = j;
        }
        else j = f[j];
    }
}

int KMP()
{
    memset(f,0,sizeof(f));
    memset(ans,0,sizeof(ans));
    int i = 0, j = 0, temp = 1;
    slen = s.length();
    alen = a.length();
    getFail();
    while (i < slen)
    {
        if (j == -1 || s[i] == a[j])
        {
            i++;
            j++;
        }
        else j = f[j];
        if (j == alen)
        {
            ans[temp] = i - alen;
            temp++;
        }
    }
    return temp - 1; //成功个数
}

int main()
{
    cin >> s >> a;
    int ansnum = KMP();
    return 0;
}

扩展KMP

/*
* 扩展KMP
* next[i]:x[i...m-1]的最长公共前缀
* extend[i]:y[i...n-1]与x[0...m-1]的最长公共前缀
*/
void preEKMP(char x[], int m, int next[])
{
    next[0] = m;
    int j = 0;
    while (j + 1 < m && x[j] == x[j + 1]) j++;
    next[1] = j;
    int k = 1;
    for (int i = 2; i < m; i++)
    {
        int p = next[k] + k - 1;
        int L = next[i - k];
        if (i + L < p + 1) next[i] = L;
        else
        {
            j = std::max(0, p - i + 1);
            while (i + j < m && x[i + j] == x[j]) j++;
            next[i] = j;
            k = i;
        }
    }
}

void EKMP(char x[], int m, char y[], int n, int next[], int extend[])
{
    preEKMP(x, m, next);
    int j = 0;
    while (j < n && j < m && x[j] == y[j]) j++;
    extend[0] = j;
    int k = 0;
    for (int i = 1; i < n; i++)
    {
        int p = extend[k] + k - 1;
        int L = next[i - k];
        if (i + L < p + 1) extend[i] = L;
        else
        {
            j = std::max(0, p - i + 1);
            while (i + j < n && j < m && y[i + j] == x[j]) j++;
            extend[i] = j;
            k = i;
        }
    }
}

AC自动机

快速版

//适用于小写字母
//统计单词出现次数或者个数
//较快
struct Aho_Corasick_Automaton
{
    #define N 500010 //单词的长度*单词个数
    queue<int> q;
    int c[N][26],val[N],fail[N],cnt=0;
    void init()
    {
        memset(c,0,sizeof(c));
        memset(val,0,sizeof(val));
        memset(fail,0,sizeof(fail));
        cnt=0;
    }
    void ins(char *s)
    {
        int len=strlen(s);
        int now=0;
        for (int i=0; i<len; i++)
        {
            int v=s[i]-'a'; 
            if (!c[now][v])c[now][v]=++cnt;
            now=c[now][v];
        }
        val[now]++;
    }
    void build()
    {
        for (int i=0; i<26; i++)
            if (c[0][i]) fail[c[0][i]]=0,q.push(c[0][i]);
        while (!q.empty())
        {
            int u=q.front();
            q.pop();
            for (int i=0; i<26; i++)
                if (c[u][i]) fail[c[u][i]]=c[fail[u]][i],q.push(c[u][i]);
                else c[u][i]=c[fail[u]][i];
        }
    }
    int query(char *s)
    {
        int len=strlen(s);
        int now=0,ans=0;
        for (int i=0; i<len; i++)
        {
            now=c[now][s[i]-'a'];
            //每个单词出现次数最多为1
            for (int t=now; t&&~val[t]; t=fail[t]) ans+=val[t],val[t]=-1;
            //每个单词出现次数最多为不限
            //for (int t=now; t; t=fail[t]) ans+=val[t];
        }
        return ans;
    }
} AC;
char p[1000005]; //缓冲区

void AUTO()
{
    int T;
    scanf("%d",&T);
    while (T--)
    {
        int n;
        scanf("%d",&n);
        AC.init();
        for (int i=1; i<=n; i++) scanf("%s",p),AC.ins(p);
        AC.build();
        scanf("%s",p);
        int ans=AC.query(p);
        printf("%d\n",ans);
    }
}

完整版

//适用字符多
//答案详见输出
//较慢
struct Aho_Corasick
{
    const static int TEXTNUM = 500 + 50; //单词数量
    const static int TEXTLEN = 250; //单词长度
    const static int maxnode = TEXTNUM * TEXTLEN; //节点数
    const static int type = 128; //单词字符数

    char str[TEXTNUM * TEXTLEN * 100]; //缓冲区
    char ss[TEXTNUM][TEXTLEN]; //单词
    int num[TEXTNUM]; //单词出现次数
    int next[maxnode][type], fail[maxnode], end[maxnode];
    int root, L;

    int newnode()
    {
        for (auto i = 0; i < type; i++) next[L][i] = -1;
        end[L++] = -1;
        return L - 1;
    }

    void init()
    {
        L = 0;
        root = newnode();
        memset(str, 0, sizeof(str));
        memset(ss, 0, sizeof(ss));
        memset(num, 0, sizeof(num));
    }

    void insert(char* str, int idx)
    {
        auto len = strlen(str);
        int now = root;
        for (auto i = 0; i < len; i++)
        {
            int id = str[i];
            if (next[now][id] == -1) next[now][id] = newnode();
            now = next[now][id];
        }
        end[now] = idx;
    }

    void build()
    {
        queue<int> Q;
        fail[root] = root;
        for (auto i = 0; i < 128; i++)
            if (next[root][i] == -1) next[root][i] = root;
            else
            {
                fail[next[root][i]] = root;
                Q.push(next[root][i]);
            }

        while (!Q.empty())
        {
            auto now = Q.front();
            Q.pop();
            for (auto i = 0; i < type; i++)
                if (next[now][i] == -1) next[now][i] = next[fail[now]][i];
                else
                {
                    fail[next[now][i]] = next[fail[now]][i];
                    Q.push(next[now][i]);
                }
        }
    }

    void query(char* str, int n)
    {
        auto len = strlen(str);
        int now = root;
        memset(num, 0, sizeof(num));
        for (auto i = 0; i < len; i++)
        {
            int id = str[i];
            now = next[now][id];
            int temp = now;
            while (temp != root)
            {
                if (end[temp] != -1) num[end[temp]]++;
                temp = fail[temp];
            }
        }
    }

    void output(int n)
    {
        int ansnum = 0, anstime = 0;
        for (int i = 1; i <= n; i++)
            if (num[i] > 0)
            {
                ansnum++;
                anstime += num[i];
                printf("%s times: %d\n", ss[i], num[i]);
            }
        printf("texts num: %d\n", ansnum); //每个单词出现次数最多为1
        printf("texts times: %d\n", anstime); //每个单词出现次数最多为无限
    }

    bool output1(int n, int id)
    {
        auto flag = false;

        for (auto i = 1; i <= n; i++)
            if (num[i] > 0)
            {
                if (!flag)
                {
                    cout << "String " << id << ":"; // 匹配成功的串编号
                    flag = true;
                }
                cout << " " << i; // 匹配到的原串编号
            }

        if (flag)
        {
            cout << endl;
            return true;
        }

        return false;
    }
} AC;

void AUTO()
{
    int n;
    while (scanf("%d", &n) != EOF)
    {
        AC.init();
        for (int i = 1; i <= n; i++)
        {
            scanf("%s", AC.ss[i]);
            AC.insert(AC.ss[i], i);
        }
        AC.build();
        scanf("%s", AC.str);
        AC.query(AC.str, n);
        AC.output(n);
    }
}


void AUTO1()
{
    int n;
    cin >> n;

    AC.init();
    for (auto i = 1; i <= n; i++)
    {
        cin >> AC.ss[i];
        AC.insert(AC.ss[i], i);
    }
    AC.build();

    int m;
    cin >> m;

    auto total = 0;

    for (auto i = 1; i <= m; i++)
    {
        cin >> AC.str;
        AC.query(AC.str, n);
        if (AC.output1(n, i)) total++;
    }

    cout << "total: " << total << endl; // 匹配成功数量
}

最长上升子序列 LIS

动态规划

直接 DP 问题不大，注意一下给你的如果是个空数组就行了

对于位置 i ，dp[i] 表示以 nums[i] 结尾的 LIS 的长度

所以初始化 dp[i]=1, 1<=i<=n 毕竟每个位置自身就是长度为1的 LIS

对于位置 i ，dp[i] 一定是由前面的结尾的值小于 nums[i] 的位置转移过来的

所以 dp[i]=max(dp[j]+1), 1<=j<i, a[j]<a[i]

$O(n^2)$ 的时间， $O(n)$ 的空间，最长不降子序列加等号就行

class Solution
{
public:
    int lengthOfLIS(vector<int>& nums)
    {
        vector<int> dp(nums.size(), 1);

        for (auto i = 0; i < nums.size(); i++)
            for (auto j = 0; j < i; j++)
                if (nums[i] > nums[j]) dp[i] = max(dp[i], dp[j] + 1);

        auto ans = 0;
        for (auto it : dp) ans = max(ans, it);

        return ans;
    }
};

二分查找优化

有一个题解是这样说的，道理是这个道理，然而我不知道为什么这样是对的：

新建数组 cell，用于保存最长上升子序列
对原序列进行遍历，将每位元素二分插入 cell 中
如果 cell 中元素都比它小，将它插到最后
否则，用它覆盖掉比它大的元素中最小的那个。
总之，思想就是让 cell 中存储比较小的元素。这样，cell 未必是真实的最长上升子序列，但长度是对的。

当然还有一个我能理解的办法，不然我也不会写这个东西了

这个办法的核心是维护一个数组，d[i] 表示长度为 i 的 LIS 的末尾元素的最小值，初始化 d1=nums[0] 。同时维护一个变量 len 标记目前的 LIS 长度

遍历数组，对于每一个元素 nums[i]：

如果这个元素大于已知的最长 LIS 的末尾元素，那么我们就找到了一个更长的 LIS ，因此 len++, d[len]=nums[i]
否则二分查找数组 d ，找到第一个比 nums[i] 小的位置 j，j 就是这个元素前面能用的最大 LIS 长度，d[j+1] 肯定是大于nums[i] ，那么现在长度为 j+1 的 LIS 末尾元素最小值就应该是 nums[i]，d[j+1]=nums[i]

这样操作数组 d 肯定是单调的，所以可以用二分查找

class Solution
{
public:
    int lengthOfLIS(vector<int>& nums)
    {
        if (nums.empty()) return 0;

        vector<int> d(nums.size() + 1, 0);
        auto len = 1;
        d[1] = nums[0];

        for (auto it : nums)
        {
            if (it > d[len])
            {
                len++;
                d[len] = it;
            }
            else
            {
                const auto index = lower_bound(d.begin() + 1, d.begin() + 1 + len, it) - d.begin();
                d[index] = it;
            }
        }

        return len;
    }
};

后缀数组

//rrank:rrank[i]为起始位置为i的后缀的排名，i:[0,len)
// sa:sa[i]为排名为i的后缀的起始位置，i:[0,len)
//height:height[i]排名为i和i-1的后缀的lcp，i:(0,len)

const int maxn = 233333;
char s[maxn];
int t1[maxn], t2[maxn], cc[maxn], x[maxn], sa[maxn], rrank[maxn], height[maxn];
int len;
bool cmp(int *y, int a, int b, int k)
{
    int a1 = y[a];
    int b1 = y[b];
    int a2 = a + k >= len ? -1 : y[a + k];
    int b2 = b + k >= len ? -1 : y[b + k];
    return a1 == b1 && a2 == b2;
}

int make_sa()
{
    int *x = t1, *y = t2;
    int m = 256;
    for (int i = 0; i < m; i++) cc[i] = 0;
    for (int i = 0; i < len; i++) ++cc[x[i] = s[i]];
    for (int i = 1; i < m; i++) cc[i] += cc[i - 1];
    for (int i = len - 1; i >= 0; i--) sa[--cc[x[i]]] = i;
    for (int k = 1; k <= len; k <<= 1)
    {
        int p = 0;
        for (int i = len - k; i < len; i++) y[p++] = i;
        for (int i = 0; i < len; i++)
            if (sa[i] >= k) y[p++] = sa[i] - k;

        for (int i = 0; i < m; i++) cc[i] = 0;
        for (int i = 0; i < len; i++) ++cc[x[y[i]]];
        for (int i = 1; i < m; i++) cc[i] += cc[i - 1];
        for (int i = len - 1; i >= 0; i--) sa[--cc[x[y[i]]]] = y[i];

        swap(x, y);
        m = 1;
        x[sa[0]] = 0;
        for (int i = 1; i < len; i++)
            x[sa[i]] = cmp(y, sa[i], sa[i - 1], k) ? m - 1 : m++;
        if (m >= len) break;
    }
    return 0;
}

void make_height()
{
    for (int i = 0; i < len; i++) rrank[sa[i]] = i;
    height[0] = 0;
    int k = 0;
    for (int i = 0; i < len; i++)
    {
        if (!rrank[i]) continue;
        int j = sa[rrank[i] - 1];
        if (k) k--;
        while (s[i + k] == s[j + k]) k++;
        height[rrank[i]] = k;
    }
}

void init()
{
    memset(s, 0, sizeof(s));
    memset(t1, 0, sizeof(t1));
    memset(t2, 0, sizeof(t2));
    memset(cc, 0, sizeof(cc));
    memset(x, 0, sizeof(x));
    memset(sa, 0, sizeof(sa));
    memset(rrank, 0, sizeof(rrank));
    memset(height, 0, sizeof(height));
    scanf("%s", s);
    len = strlen(s);
    make_sa();
    make_height();
}

编辑距离

定义

编辑距离（Edit Distance），又称 Levenshtein 距离。

编辑距离是指两个字符串之间，由一个字符串转化为另一个字符串所需的最小编辑操作次数。

许可的编辑操作包括：

在原串中添加一个字符
在原串中删除一个字符
在原串中修改一个字符

解法

解法当然是 DP 了！

先来看看操作，设原串为 A 新串为 B，A 串的长度为 n，B 串的长度为 m，那么现在就有对两个串的 6 种操作。

然而我们可以把操作简化为三种：

在 A 中添加一个字符（等价于在 B 中删除一个字符）
在 B 中添加一个字符（等价于在 A 中删除一个字符）
在 A 中修改一个字符（等价于在 B 中修改一个字符）

然后看看转移，这里用 dp[i][j] 表示 A 从头开始的 i 个字符与 B 从头开始的 j 个字符。

i 和 j 为 0 的时候就表示空串。所以这个二维数组应该开到 dp[n + 1][m + 1] 。

对于 dp[i][j] 可以由下面三种方式转移得到：

dp[i - 1][j] + 1 只需要在现有 A 串的末尾添加一个字符即可
dp[i][j - 1] + 1 只需要在现有 B 串的末尾添加一个字符即可
dp[i - 1][j - 1] + (A[i - 1] == B[i - 1] ? 0 : 1) 这里需要判断 A 串中第 i 个字符（下标 i - 1）和 B 串中第 j 个字符（下标 j - 1）是否相同。相同的话直接转移，不同的话需要把 A[i - 1] 修改为 B[j - 1]，因此编辑距离增加 1

因此

$$
dp[i][j]=min(dp[i-1][j]+1,dp[i][j-1]+1,dp[i][j]+(A[i - 1] == B[i - 1] ? 0 : 1))
$$

最后看看边界条件，由于空串到任意一个串只需要不断加加加，一个串到空串只需要不断减减减，所以：

dp[i][0] = i 在 B 中添加 i 个字符
dp[0][j] = j 在 A 中添加 j 个字符

条件齐了，将 i 和 j 从 0 推到 n 和 m 即可，正推时所有前置条件都已经算完了。

时空复杂度均为 $O(nm)$。

实现

class Solution
{
public:
    int minDistance(string word1, string word2)
    {
        vector<vector<int>> dp(word1.size() + 1, vector<int>(word2.size() + 1));

        for (auto i = 0; i < dp.size(); i++) dp[i][0] = i;
        for (auto j = 0; j < dp[0].size(); j++) dp[0][j] = j;

        for (auto i = 1; i < dp.size(); i++)
            for (auto j = 1; j < dp[0].size(); j++)
                dp[i][j] = min({
                    dp[i - 1][j] + 1,
                    dp[i][j - 1] + 1,
                    dp[i - 1][j - 1] + (word1[i - 1] == word2[j - 1] ? 0 : 1)
                });

        return dp[word1.size()][word2.size()];
    }
};

排序

快速排序

// 0下标
void quicksort(int b, int e, int a[])
{
    auto i = b, j = e, x = a[(b + e) / 2];
    do
    {
        while (a[i] < x) i++;
        while (a[j] > x) j--;
        if (i <= j) swap(a[i++], a[j--]);
    }
    while (i < j);
    if (i < e) quicksort(i, e, a);
    if (j > b) quicksort(b, j, a);
}

void quicksort(int b, int e, vector<int>& a)
{
    auto i = b, j = e, x = a[(b + e) / 2];
    do
    {
        while (a[i] < x) i++;
        while (a[j] > x) j--;
        if (i <= j) swap(a[i++], a[j--]);
    }
    while (i < j);
    if (i < e) quicksort(i, e, a);
    if (j > b) quicksort(b, j, a);
}

// 开始选中间的数为 flag，把 flag 位置和最后一个位置交换
// lpos 为比 flag 小的最后一个位置，rpos 从 L 扫到 R-1，遇到一个比 flag 小的就 lpos++，交换 lpos 和 rpos
// 一轮完了 lpos++，此时的 lpos 为 flag 的正确位置，交换 lpos 和 R
// 递归处理 L 到 lpos-1 和 lpos+1 到 R
void qksort(const int L, const int R, vector<int>& v)
{
    if (L >= R) return;
    const auto flag = v[(L + R) / 2];
    swap(v[R], v[(L + R) / 2]);

    auto lpos = L - 1;
    for (auto rpos = L; rpos < R; rpos++)
        if (v[rpos] < flag)
        {
            lpos++;
            swap(v[lpos], v[rpos]);
        }

    lpos++;
    swap(v[lpos], v[R]);

    qksort(L, lpos - 1, v);
    qksort(lpos + 1, R, v);
}

归并排序

const int MAXN = 200000;
int a[MAXN];//待排序
int t[MAXN];//额外空间

void msort(int b, int e)
{
    if (e - b <= 0) return;
    int mid = (b + e) / 2, p1 = b, p2 = mid + 1, i = b;
    msort(b, mid);
    msort(mid + 1, e);
    while (p1 <= mid || p2 <= e)
    {
        if (p2 > e || (p1 <= mid && a[p1] <= a[p2])) t[i++] = a[p1++];
        else t[i++] = a[p2++];
    }
    for (int i = b; i <= e; i++) a[i] = t[i];
}

搜索

N皇后

void queen()
{
    int n, i, odd;
    while (cin >> n)
    {
        if (n < 4) cout << "Impossible";
        else if ((n / 2) % 3 != 1)
        {
            cout << 2;
            for (i = 4; i <= n; i += 2) cout << " " << i;
            for (i = 1; i <= n; i += 2) cout << " " << i;
        }
        else
        {
            if (n % 2 == 0) odd = 0;
            else
            {
                n--;
                odd = 1;
            }
            cout << n / 2;
            for (i = n / 2 + 1; i != n / 2 - 1; i = (i + 2) % n) cout << " " << i + 1;
            for (i = (i + n - 2) % n; i != n / 2 - 1; i = (i + n - 2) % n) cout << " " << n - i;
            cout << " " << n - i;
            if (odd) cout << " " << n + 1;
        }
        cout << endl;
    }
}

BFS 队列版本

typedef pair<int, int> P; //点的坐标
char map[MAXN][MAXM]; //地图数组
int n, m; //地图行列数
int start_s, start_y, end_x, end_y; //起点终点坐标
int d[MAXN][MAXM] = {0}; //记录走到该坐标需要的最短步数

void bfs()
{
    queue<P> q;
    q.push(P(start_s, start_y)); //将起点放进队列中
    d[start_s][start_y] = 0; //到起点步数为0

    while (!q.empty())
    {
        P p = q.front(); //定义当前队列顶端坐标为P
        q.pop();//将P弹出 @
        if (p.first == end_x && p.second == end_y) break;//判断该坐标是否是终点，是的话结束
        for (int i = 0; i < 4; i++)//使坐标不断向四个方向移动
        {
            int x = p.first + dx[i];
            int y = p.second + dy[i];
            if (0 <= x && x < n && 0 <= y && y <= m && map[x][y] != '#' && d[x][y] == 0)
            {
                //当前坐标某方位是否可移动判断
                q.push(P(x, y)); //如果坐标当前某方向可移动，则将该位置该点坐标放入队列中
                d[x][y] = d[p.first][p.second] + 1; //记录该位置的最短步数 = 上一位置到达步数 + 1
            }
            //如果四个方位都不行则将顶点位置弹出，直到返回上一个有多个出口的位置
        }
    }
}

C++

引用

//引用(reference)为对象起了另一个名字，将引用与初始值绑定(bind)在一起，二者类型需相同
//引用及别名
//必须初始化，初始化后无法重新绑定
//使用 &d 其中d为变量
int a;
char b;
int &aa = a;
auto &bb = b;//auto将自动识别类型 C++11

范围for

//C++ 11
//for (变量 : 序列) 语句
//范围for可以在不知道开始和结尾的情况下进行遍历
//序列均可返回迭代器的begin和end成员
//可以为 初始值列表({1,2,3}) 数组 string vector map set...

//声明变量若未使用引用，则只读不可写
map<int, int> map = { {1,1},{2,2} };
for (auto i : map)
    cout << i.first << endl << i.second << endl;

//使用引用，可写
for (auto &i : map) i.second++;

列表

//c++11
//循环可以使用列表，类似Python list
for (int i:{2, 3, 7, 61, 24251}) {cout<<i;}
//多个最值的比较
int x = max({ 1, 2, 3 });

二进制读写

// 将int以二进制输出（四个字节）
inline output_int(ofstream& out, int x)
{
    for (auto i = 3; i >= 0; i--)
    {
        out << *(reinterpret_cast<char*>(&x) + i);
    }
}

// 将int以二进制输入（四个字节）
inline int input_int(ifstream& in)
{
    auto ans = 0;
    for (auto i = 0; i < 4; i++)
    {
        ans <<= 8;
        char temp;
        in >> temp;
        ans |= static_cast<unsigned char>(temp);
    }
    return ans;
}

头文件

< __builtin > 内建函数

__builtin_clz(x)         //返回x的二进制前导0的个数
__builtin_ctz(x)         //返回x的二进制末尾0的个数
__builtin_popcount(x)    //返回x的二进制中1的个数
__builtin_parity(x)      //返回x的二进制中1的个数的奇偶性，0偶1奇
__builtin_ffs(x)         //返回x的二进制中末尾最后一个1的位置，编号从1开始
//以上函数的long long版本：
__builtin_clzll
__builtin_ctzll
__builtin_popcountll

< cmath > 数学函数

//基础运算
abs(x)          //x的绝对值，整型
fabs(x)         //x的绝对值，浮点
ceil(x)         //x向上取整
floor(x)        //x向下取整
round(x)        //x的四舍五入值
trunc(x)        //截取x的整数部分
fmod(x, y)      //x/y的浮点数余数
//指数/对数
pow(x, y)       //x的y次幂
exp(x)          //e的x次幂
sqrt(x)         //x的平方根
cbrt(x)         //x的立方根 C++11
(int)(pow(x,1.0/3.0)+0.5) //等价，0.5用于四舍五入
log(x)          //x以e为底的对数
log10(x)        //x以10为底的对数
log2(x)         //x以2为底的对数
//三角函数
acos(x)         //x的反余弦
asin(x)         //x的反正弦
atan(x)         //x的反正切
atan2(y, x)     //点(x, y)与x轴正方向的夹角(返回值范围(-π, π])
hypot(x, y)     //返回直角三角形斜边的长度：√(x2+y^2)

< random > 随机函数

mt19937 mt_rand(time(0))        //初始化随机数生成器
mt_rand()                       //返回一个随机的unsigned int值(0 ~ 4294967295)
//法二
//<cstdlib> <ctime> 
srand((unsigned)time(NULL));
a = rand() % 9000 + 1000;

< cctype > 字符类型

isalnum()     //如果参数是字母或数字，该函数返回true
isalpha()     //如果参数是字母，该函数返回true
isdigit()     //如果参数是数字，该函数返回true
islower()     //如果参数是小写字母，该函数返回true
isupper()     //如果参数是大写字母，该函数返回true
isxdigit()    //如果参数是十六进制的数字，即0～9、a~f、A~F，该函数返回true
tolower()     //如果参数是大写字符，则返回其小写，否则返回该参数
toupper()     //如果参数是小写字母，则返回其大写，否则返回该参数

< cstring > C字符串

memset(a, 0, sizeof(a)) //将数组a清零，理论上只能将数组全部变成0或-1,其他数也行，原因未知
strlen(str)             //返回字符串str的长度（不包括'\0'）
strcpy(s1, s2)          //复制字符串 s2 到字符串 s1
strcat(s1, s2)          //把s2复制到s1已有的字符之后，形成连起的串
strchr(s1, ch)          //返回一个指针，指向字符串 s1中字符 ch 的第一次出现的位置
strstr(s1, s2)          //返回一个指针，指向字符串 s1 中字符串 s2 的第一次出现的位置
strcmp(s1, s2)          //如果相同，则返回 0；如果 s1<s2 则返回值小于 0；反之大于 0

//数字与字符串转换 C++11
string s=to_string(x)   //把数字x转换为字符串，x可以为任意数的类型
int n=stoi(s)           //把字符串s转换为int类型
long long n=stoll(s)    //把字符串s转换为long long类型

< algorithm > 算法

swap(a, b)    //交换两个变量的值。
max(a, b)     //返回两个数中的较大值。
min(a, b)     //返回两个数中的较小值。

//最值+列表，C++11
max({1,2,3})    //大括号中多个值用逗号隔开
min({1,2,3})    //大括号中多个值用逗号隔开

//以下函数对STL类型的操作，(a, a + n) 改为 (a.begin(), a.end())
max_element(a, a + n)        //返回序列中最大值的地址。序列中最大值：*max_element(a, a + n)
min_element(a, a + n)        //返回序列中最小值的地址。序列中最小值：*min_element(a, a + n)
reverse(a, a + n)            //翻转一个n个元素的数组
random_shuffle(a, a + n)     //随机打乱一个n个元素的数组
sort(a, a + n)               //对n个元素的数组进行从小到大排序
sort(a, a + n, greater<int>())               //对n个元素的数组进行从大到小排序
sort(a, a + n, [](const auto &a,const auto &b) {return a>b;})          //自定义排序，排序方法由Lambda表达式的返回值决定（这里是从大到小），c++14，此时可用auto

unique(a, a + n)             //去除序列中相邻的重复元素，返回去重后的尾地址
binary_search(a, a + n, x)   //查找有序序列中是否存在元素x，找到返回1，否则返回0
lower_bound(a, a + n, x, cmp)     //返回有序序列中第一个≥x的值的迭代器
upper_bound(a, a + n, x, cmp)     //返回有序序列中第一个>x的值的迭代器
lower_bound(a, a + n, x, cmp) - a //第一个≥x的值的数组下标
upper_bound(a, a + n, x, cmp) – a //第一个>x的值的数组下标

equal_range(a, a + n, x, cmp)     //返回pair(x,y) ,x对应value的开始迭代器，y对应value的结束迭代器，左闭右开

//取值前先判断：若不存在≥x的值，则会造成非法内存访问(Runtime Error)

//全排列
bool next_permutation(iterator start,iterator end) 
//逆序是最大的一个，为假则已经是逆序
int a[5] = { 5,4,3,2,1 };
sort(a, a + 5);//顺序是最小的一个
next_permutation(a, a + 5);//下一个
prev_permutation(a, a + 5);//前一个

< numeric > 数值序列

//使用vector时应用v.begin()和v.end()

iota(numbers, numbers + 5, -2.5)
//从2.5开始生成++的递增序列放入numbers
// Values are -2.5 -1.5 -0.5 0.5 1.5 2.5 3.5 4.5 5.5

accumulate(numbers, numbers + 5, init)
//求number的数列和 + init

inner_product(series1, series1 + 5, series2, init)
//求series1和series2的内积/叉积

adjacent_difference(numbers, numbers + 5, result)
//求相邻两个元素差放入result中

partial_sum(numbers, numbers + 5, result)
//求前缀和放入result中

int val[] = {1,2,3,4,5};
partial_sum(val, val+5, result, multiplies<int>());
//求阶乘

< utility > 二元组

pair<string, int> planet;        //定义一个<string, int>二元组
pair<int, double> p1(1, 2.4);    //声明并初始化
planet.first = "Earth";
planet.second = 6371;            //给二元组中的两个元素单独赋值
planet = {"Earth", 6371};        //给二元组整体赋值
p4 = make_pair(1, 2.4);          //赋值

< string > 字符串

s.size()
s.length()      //字符串s的长度
s.clear()       //清空字符串s
s.erase(a,b);   //从下标a开始，删除b个字符
s.find(s1)      //返回字符串s1在s中第一次出现的位置，如果没有则返回-1
s.rfind(s1)     //返回字符串s1在s中最后一次出现的位置，如果没有则返回-1
s.substr(a,b);  //从下标a开始，生成长度为b的子串
//可以直接比较，字典序

< bitset > 01数组

bitset<10000> s;   //定义一个10000位二进制数，<>中填写位数。
~, &, |, ^         //按位与、或、异或
<<、>>             //左移、右移
==、!=             //比较两个bitset是否相等
s[k]               //表示s的第k位，最低位是第0位
s.count()          //返回s中有多少位为1。
s.any()
s.none()
//若s所有位都为0，则s.any()返回false，s.none()返回true
//若s至少一位为1，则s.any()返回true，s.none()返回false
s.set() / s.reset() / s.flip()
//把s的所有位变为1 / 变为0 / 取反

< iterator > 迭代器

//迭代器为指针
//该头文件实际可以不带
//用迭代器it遍历容器中的元素（这里it是指向当前元素的指针）
for (auto it = A.begin(); it != A.end(); it++) cout<<*it<<endl;

< vector > 动态数组

vector<vector<int>> v;            //二维整型动态数组
vector<int> v1[n];                //包含n个元素，二维数组
vector<vector<int>> v2(n, val);   //包含n个元素，且值为val
vector<vector<int>>::iterator it; //迭代器
//可以以字典序进行比较

v.push_back(a)             //向尾端插入a
v.emplace_back(a)          //向尾端插入a，c++11优化版，可以自动组成pair
v.pop_back()               //删除尾端元素
v.empty()                  //为空返回真
v.size()                   //返回元素个数
v.clear()                  //清空
v.front()                  //返回首元素值的引用
v.back()                   //返回尾元素值的引用
v.begin()                  //首元素指针
v.end()                    //v的尾元素的下一位置指针
v.rbegin()                 //尾元素指针
v.end()                    //v的首元素上一位置指针
v.insert(it,i)             //在迭代器it位置插入插入元素i
v.emplace(it,i)            //在迭代器it位置插入插入元素i，优化版
v1 = v2;                   //用v2中的元素拷贝替换v1
v[i][j]                    //引用，但不能以此方法添加
reverse(v.begin(),v.end());//翻转数组

//排序后可以二分查找，返回迭代器，指向第一个不小于k的元素，O(n)
lower_bound(v.begin(), v.end(), k, cmp)  
//排序后可以二分查找，返回迭代器，指向第一个大于k的元素，O(n)
upper_bound(v.begin(), v.end(), k, cmp)  

//将数组里的元素随机排列，概率相同，O(n)
random_shuffle(v.begin(), v.end());

//元素去重并删除，需要先排序
v.erase(unique(v.begin(), v.end()), v.end());

< map > 映射表

//map
//key-value组成，key唯一，升序排列
//value为数的时候，初始化可能不为0，需要clear（出现情况未知）
//遍历时key为const
//八倍常数
//不要使用数组下标m[i]进行访问，如果没有这个元素会自动创建，导致大小改变

map<int, int> m = { {1,3} };        //初始化
m.insert({ 2,3 })                   //插入元素
m.insert(b, e)                      //插入迭代器从b到e，返回值为成功数量
m.emplcace({ 2,3 })                 //插入元素，优化版
m[3] = 4                            //插入元素或者更改元素
m.empty()                           //为空返回真
m.size()                            //返回元素个数
m.clear()                           //清空
m.find(k)                           //寻找第一个关键值k，失败返回m.end()
m.count(k)                          //统计关键值k的数量
m.begin()                           //m的首元素（key值最小记录）指针
m.end()                             //m的尾元素（key值最大记录）的下一位置指针
m.rbegin()                          //m的尾元素（key值最大记录）指针
m.rend()                            //m的首元素（key值最小记录）的上一位置指针
m.erase(k)                          //删除元素k
map<int, int>::iterator it;         //迭代器，->first ->second引用
m.erase(it, it + 5);                //删除元素并改变长度，删除后要重置迭代器，返回值为删除成功的数量
m.lower_bound(k);                   //二分查找，返回迭代器，指向第一个不小于k的元素
m.upper_bound(k);                   //二分查找，返回迭代器，指向第一个大于k的元素

//unordered_map 无序的映射，基本同map
unordered_map<int> m;

//multimap 可重复的映射，一个key值对应多个value，并存放在一起，基本同map
multimap<int> m;
m.equal_range(x);                   //返回pair(x,y) ,x对应value的开始迭代器，y对应value的结束迭代器，左闭右开

//unordered_multimap 无序可重复的映射，基本同map
unordered_multimap<int> m;

< set > 集合

//set
//key组成，key唯一，升序排列
//遍历时key为const
set<int> s = { 1,3 }      //初始化
set<int,less<int>> s;     //初始化降序排列
set<int,greater<int>> s;  //初始化升序排列
s.insert({ 2,3 })         //插入元素
s.emplcace({ 2,3 })       //插入元素，优化版
s.insert(b, e)            //插入迭代器从b到e，返回值为成功数量
s.empty()                 //为空返回真
s.size()                  //返回元素个数
s.clear()                 //清空
s.find(k)                 //寻找第一个关键值k，失败返回s.end()
s.count(k)                //统计关键值k的数量
s.begin()                 //s的首元素（最小元素）指针
s.end()                   //s的尾元素（最大元素）的下一位置指针
s.rbegin()                //s的尾元素（最大元素）指针
s.rend()                  //s的首元素（最小元素）的上一位置指针
set<int>::iterator it；   //迭代器
s.erase(it, it + 5)       //删除元素并改变长度，删除后需重置迭代器，返回值为删除成功的数量
s.lower_bound(k)          //二分查找，返回迭代器，指向第一个不小于k的元素
s.upper_bound(k)          //二分查找，返回迭代器，指向第一个大于k的元素
set_union(A.begin(), A.end(), B.begin(), B.end(), C.begin())
//将集合A和集合B取并集存入集合C中，记得清空用于存放的集合
set_intersection(A.begin(), A.end(), B.begin(), B.end(), C.begin())
//将集合A和集合B取交集存入集合C中，记得清空用于存放的集合

//unordered_set 无序的集合，基本同set
unordered_set<int> s = { 1,3 };

//multiset 可重复的集合，基本同set
multiset<int> s = { 1,3,3 };

//unordered_multiset 无序可重复的集合，基本同set
unordered_multiset<int> s = { 1,3,3 };

//自定义set，需要重载运算符
struct set_type
{
    int num;
    friend bool operator < (const set_type& x, const set_type& y)
    {
        return x.num < y.num;
    }
};
set<set_type> s;

< stack > 栈

stack<int> s;  //定义一个int类型的栈
s.push(x)      //将元素x压入栈顶
s.pop()        //弹出栈顶元素
s.top()        //访问栈顶元素
s.empty()      //判断栈s是否为空
s.size()       //栈s中的元素个数

< queue> 队列

//先进先出队列
queue<int> q;   //定义一个int类型的队列
q.push(x)       //将元素x放入队尾
q.pop()         //移除队首元素
q.front()       //访问队首元素
q.back()        //访问队尾元素
q.empty()       //判断队列q是否为空
q.size()        //队列q中的元素个数

//优先队列/堆
//int类型，大的优先，从大到小取出数值的优先队列（堆）
priority_queue<int> q;
//int类型，小的优先，从小到大取出数值的优先队列（堆）
priority_queue<int, vector<int>, greater<int>> q;
//int类型，小的优先，自定义顺序
struct cmp1 { bool operator ()(int &a, int &b) { return a > b; } };
priority_queue<int, vector<int>, cmp1>pq3;

auto cmp = [](const auto& x, const auto& y)
{
    return x.first > y.first;
};
priority_queue<pair<int, int>, vector<pair<int, int>>, decltype(cmp)> pq(cmp);

q.push(x)       //将元素x放入队列（堆）中
q.pop()         //移除堆顶元素
q.top()         //访问堆顶元素
q.empty()       //判断堆q是否为空
q.size()        //堆q中的元素个数

//deque 双向队列
//两边都是开口的，均可进可出
//基本操作同queue
deque<int> dq;
dq.front()              //访问首端元素
dq.back()               //访问尾端元素
dq.push_front(i)        //首端压入i
dq.emplace_front(i)     //首端压入i，c++11优化版
dq.push_back(i)         //尾端压入i
dq.emplace_back(i)      //尾端压入i，c++11优化版
dq.pop_fron()           //首端弹出元素
dq.pop_back()           //尾端弹出元素

Python

输入

#存放列表
a=[]

#整数
for x in input().split():
    a.append(int(x))

#浮点数
for x in input().split():
    a.append(float(x))
    
    
#读
with open('C:/Users/dongs/Desktop/qwer.txt', 'r', encoding = 'utf-8') as cin:
    L = cin.readlines()
    for lines in L:
        x = lines.split()[-1]

#写
with open('C:/Users/dongs/Desktop/test.txt', 'w', encoding = 'utf-8') as cout:
    cout.write('!')

留坑

尺取法
威佐夫
nim K
容斥原理
隔板法
斯特林数（第一类第二类）
矩阵快速幂
高斯消元
等价类计数
卡特兰数应用
Lucas定理
莫比乌斯反演
矩阵运算
矩阵快速幂
母函数
NTT
回文自动机
莫比乌斯函数反演
字典树
线段树
堆

make_heap(v.begin(),v.end(), cmp);//创建堆，无cmp时默认大根堆
sort_heap(v.begin(),v.end());     //堆排序
push_heap(v.begin(),v.end());     //先push一个元素到v的最后，再调用该函数
pop_heap(v.begin(),v.end());      //把堆顶元素和最后一个元素，然后维护堆，对顶元素仍可访问

无存在感小透明